题目内容
20.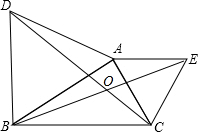 如图,△ABD、△AEC都是等边三角形,BE=4cm,求DC.
如图,△ABD、△AEC都是等边三角形,BE=4cm,求DC.
分析 由等边三角形的性质得出AB=AD,AE=AC,∠BAD=∠CAE=60°,证出∠BAE=∠DAC,根据SAS证明△ABE≌△ADC,得出对应边相等即可.
解答 解:∵△ABD、△AEC都是等边三角形,
∴AB=AD,AE=AC,∠BAD=∠CAE=60°,
∴∠BAE=∠DAC,
在△ABE和△ADC中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠DAC}\\{AE=AC}\end{array}\right.$,
∴△ABE≌△ADC(SAS),
∴BE=DC=4cm.
点评 本题考查了等边三角形的性质、全等三角形的判定与性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
12.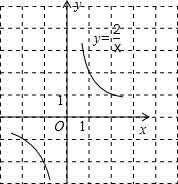 函数y=$\frac{2}{x}$的图象如图所示,在同一直角坐标系内,如果将直线y=-x+1沿y轴向上平移2个单位后,那么所得直线与函数y=$\frac{2}{x}$的图象的交点共有( )个.
函数y=$\frac{2}{x}$的图象如图所示,在同一直角坐标系内,如果将直线y=-x+1沿y轴向上平移2个单位后,那么所得直线与函数y=$\frac{2}{x}$的图象的交点共有( )个.
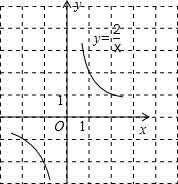 函数y=$\frac{2}{x}$的图象如图所示,在同一直角坐标系内,如果将直线y=-x+1沿y轴向上平移2个单位后,那么所得直线与函数y=$\frac{2}{x}$的图象的交点共有( )个.
函数y=$\frac{2}{x}$的图象如图所示,在同一直角坐标系内,如果将直线y=-x+1沿y轴向上平移2个单位后,那么所得直线与函数y=$\frac{2}{x}$的图象的交点共有( )个.| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
10.从2名男生和3名女生中随机抽取1名2015年苏州世乒赛志愿者,恰好抽到女生的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
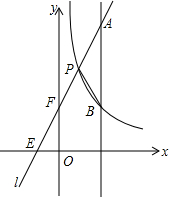 如图,一次函数y1=kx+b的图象l与坐标轴分别交于点E、F,与函数y2=$\frac{4}{x}$(x>0)的图象交于点P(1,m),且F是PE的中点
如图,一次函数y1=kx+b的图象l与坐标轴分别交于点E、F,与函数y2=$\frac{4}{x}$(x>0)的图象交于点P(1,m),且F是PE的中点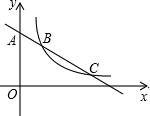 如图,直线y=一$\frac{{\sqrt{3}}}{3}$x+b与y轴交于点A,与双曲线y=$\frac{k}{x}$在第一象限交于B、C两点,且AB•AC=12,则k值为3$\sqrt{3}$.
如图,直线y=一$\frac{{\sqrt{3}}}{3}$x+b与y轴交于点A,与双曲线y=$\frac{k}{x}$在第一象限交于B、C两点,且AB•AC=12,则k值为3$\sqrt{3}$. 如图,在?ABCD中,EF∥BC,MN∥CD,EF与MN相交于点O,除外,图中还有8个平行四边形.
如图,在?ABCD中,EF∥BC,MN∥CD,EF与MN相交于点O,除外,图中还有8个平行四边形.