题目内容
3.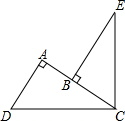 如图,∠DCE=90°,∠DAC=90°,BE⊥AC于点B,且DC=EC,请证明:AB+AD=BE.
如图,∠DCE=90°,∠DAC=90°,BE⊥AC于点B,且DC=EC,请证明:AB+AD=BE.
分析 利用同角的余角相等得到一对角相等,再由一对直角相等,CD=CE,利用AAS得到三角形ECB与三角形CDA全等,利用全等三角形对应边相等得到BC=AD,BE=AC,由AB+BC=AC=BE,等量代换即可得证.
解答 证明:∵∠ECB+∠DCA=90°,∠DCA+∠D=90°,
∴∠ECB=∠D,
在△ECB和△CDA中,
$\left\{\begin{array}{l}{∠ECB=∠D}\\{∠EBC=∠A=90°}\\{CE=CD}\end{array}\right.$,
∴△ECB≌△CDA(AAS),
∴BC=AD,BE=AC,
∴AD+AB=AB+BC=AC=BE.
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
12.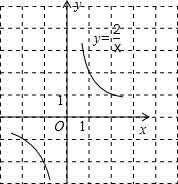 函数y=$\frac{2}{x}$的图象如图所示,在同一直角坐标系内,如果将直线y=-x+1沿y轴向上平移2个单位后,那么所得直线与函数y=$\frac{2}{x}$的图象的交点共有( )个.
函数y=$\frac{2}{x}$的图象如图所示,在同一直角坐标系内,如果将直线y=-x+1沿y轴向上平移2个单位后,那么所得直线与函数y=$\frac{2}{x}$的图象的交点共有( )个.
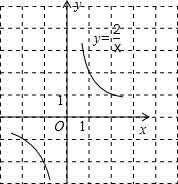 函数y=$\frac{2}{x}$的图象如图所示,在同一直角坐标系内,如果将直线y=-x+1沿y轴向上平移2个单位后,那么所得直线与函数y=$\frac{2}{x}$的图象的交点共有( )个.
函数y=$\frac{2}{x}$的图象如图所示,在同一直角坐标系内,如果将直线y=-x+1沿y轴向上平移2个单位后,那么所得直线与函数y=$\frac{2}{x}$的图象的交点共有( )个.| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
13.下列说法正确的是( )
| A. | 一个游戏中奖的概率是$\frac{1}{500}$,则做500次这样的游戏一定会中奖 | |
| B. | 了解50发炮弹的杀伤半径,应采用普查的方式 | |
| C. | 一组数据1,2,3,2,3的众数和中位数都是2 | |
| D. | 数据:1,3,5,5,6的方差是3.2 |
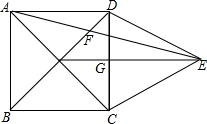 如图所示,四边形ABCD是正方形,△DCE是等边三角形,AC、BD交于点O,连接AE交BD于F,连接OE交CD于G
如图所示,四边形ABCD是正方形,△DCE是等边三角形,AC、BD交于点O,连接AE交BD于F,连接OE交CD于G 如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D,若S△OCD=6,则S△OBD的值为4.
如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D,若S△OCD=6,则S△OBD的值为4. 在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图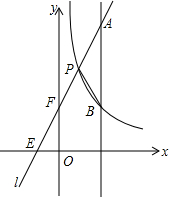 如图,一次函数y1=kx+b的图象l与坐标轴分别交于点E、F,与函数y2=$\frac{4}{x}$(x>0)的图象交于点P(1,m),且F是PE的中点
如图,一次函数y1=kx+b的图象l与坐标轴分别交于点E、F,与函数y2=$\frac{4}{x}$(x>0)的图象交于点P(1,m),且F是PE的中点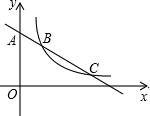 如图,直线y=一$\frac{{\sqrt{3}}}{3}$x+b与y轴交于点A,与双曲线y=$\frac{k}{x}$在第一象限交于B、C两点,且AB•AC=12,则k值为3$\sqrt{3}$.
如图,直线y=一$\frac{{\sqrt{3}}}{3}$x+b与y轴交于点A,与双曲线y=$\frac{k}{x}$在第一象限交于B、C两点,且AB•AC=12,则k值为3$\sqrt{3}$.