题目内容
14. 如图,△ABC中,AB=AC.
如图,△ABC中,AB=AC.(1)(尺规作图)作∠ABC的平分线,交AC于D;
(2)如果由(1)所得的角平分线BD=AD,
①求∠A的度数;②求证:△BCD是等腰三角形.
分析 (1)直接利用角平分线的作法得出得出答案;
(2)①利用角平分线的性质结合三角形内角和定理得出答案;
②利用等腰三角形的性质与判定方法得出BD=CB,进而得出答案.
解答  解:(1)如图所示:BD即为所求;
解:(1)如图所示:BD即为所求;
(2)①∵BD=AD,
∴∠A=∠ABD,
∵∠ABD=∠CBD,
∴设∠A=x,则∠ABD=∠DBC=x,
∵AB=AC,
∴∠ABC=∠C=2x,
∴x+2x+2x=180°,
解得:x=36°,
∴∠A=36°;
②证明:由①得,∠DBC=36°,∠C=72°,
则∠BDC=72°,
故∠C=∠BDC,
则BD=BC,
故△BCD是等腰三角形.
点评 此题主要考查了基本作图以及等腰三角形的性质与判定,正确把握等腰三角形的性质是解题关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
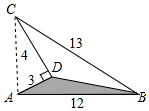 有一田地的形状和尺寸如图所示,∠ADC=90°,则阴影部分的面积为$\frac{54}{5}$.
有一田地的形状和尺寸如图所示,∠ADC=90°,则阴影部分的面积为$\frac{54}{5}$. 如图,以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,当线段AC与BC的长满足何种数量关系时,AB是小圆的切线?并说明理由.
如图,以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,当线段AC与BC的长满足何种数量关系时,AB是小圆的切线?并说明理由. 如图所示,等腰梯形ABCD中,AD∥BC,AB=8cm,AD=6cm,BC=14cm,∠B=60°,P为下底BC上一点(不与B、C重合),连接AP,过点P作PE交DC于点E,使得∠APE=∠B.
如图所示,等腰梯形ABCD中,AD∥BC,AB=8cm,AD=6cm,BC=14cm,∠B=60°,P为下底BC上一点(不与B、C重合),连接AP,过点P作PE交DC于点E,使得∠APE=∠B.