题目内容
3.在△ABC中,AB=AC=5,BC=6,则tanC=$\frac{4}{3}$.分析 作AD⊥BC,则由等腰三角形的性质可知BD的长;再根据勾股定理求出AD的长,运用锐角三角函数的定义解答.
解答  解:如图,作AD⊥BC于D点.则BD=CD=3.
解:如图,作AD⊥BC于D点.则BD=CD=3.
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴tanC=$\frac{AD}{CD}$=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查了勾股定理和锐角三角函数的定义及等腰三角形的性质,比较简单.

练习册系列答案
相关题目
5.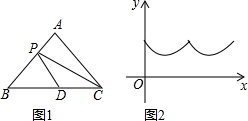 如图1,在△ABC 中,AB=AC,点D是BC的中点,点P沿B→A→C方向从点B运动到点C.设点P经过的路径长为x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
如图1,在△ABC 中,AB=AC,点D是BC的中点,点P沿B→A→C方向从点B运动到点C.设点P经过的路径长为x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
 如图1,在△ABC 中,AB=AC,点D是BC的中点,点P沿B→A→C方向从点B运动到点C.设点P经过的路径长为x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
如图1,在△ABC 中,AB=AC,点D是BC的中点,点P沿B→A→C方向从点B运动到点C.设点P经过的路径长为x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )| A. | BP | B. | AP | C. | DP | D. | CP |
2.正方形具备而矩形不具备的特征是( )
| A. | 对角线互相垂直 | B. | 对角线相等 | ||
| C. | 对角线互相平分且相等 | D. | 对角线互相平分 |
3.下列各式:①3x3•4x5=7x8,②2x3•3x3=6x9,③(x3)5=x8,④(3xy)3=9x3y3,其中正确的个数为( )
| A. | 0 个 | B. | 1个 | C. | 2个 | D. | 3个 |
 在如图所示的直角坐标系中,点C坐标为(7,3).回答下列问题:
在如图所示的直角坐标系中,点C坐标为(7,3).回答下列问题: 如图,△ABC中,AB=AC.
如图,△ABC中,AB=AC.