题目内容
6. 如图所示,等腰梯形ABCD中,AD∥BC,AB=8cm,AD=6cm,BC=14cm,∠B=60°,P为下底BC上一点(不与B、C重合),连接AP,过点P作PE交DC于点E,使得∠APE=∠B.
如图所示,等腰梯形ABCD中,AD∥BC,AB=8cm,AD=6cm,BC=14cm,∠B=60°,P为下底BC上一点(不与B、C重合),连接AP,过点P作PE交DC于点E,使得∠APE=∠B.(1)试说明:△APB∽△PCE;
(2)在底边BC上是否存在一点P,使得DE:EC=5:3?如果存在,求BP的长;如果不存在,请说明理由.
分析 (1)由等腰梯形ABCD中,AD∥BC,易得∠B=∠C,又由∠APE=∠B,可得∠BAP=∠CPE,继而证得:△APB∽△PCE;
(2)首先由DE:EC=5:3,求得CE的长,然后由设BP=xcm,则PC=BC-BP=14-x(cm),由△APB∽△PCE,根据相似三角形的对应边成比例,求得答案.
解答 (1)证明:由∠APC为△ABP的外角得:∠APC=∠B+∠BAP,
又∵∠APC=∠APE+∠CPE,∠B=∠APE,
∴∠BAP=∠CPE,
∵梯形ABCD是等腰梯形,
∴∠B=∠C,
∴△ABP∽△PCE(如果一个三角形的两个角分别与另一个三角形两个角对应相等,那么这两个三角形相似) …(8分)
(2)解:存在这样的点P.
理由如下:∵等腰梯形ABCD中,AD∥BC,AB=8cm,
∴CD=AB=8cm,
∵DE:EC=5:3,DE+CE=CD=8cm,
∴CE=$\frac{3}{8}$CD=3cm,
设BP=xcm,则PC=BC-BP=14-x(cm),
∵△ABP∽△PCE,
∴$\frac{AB}{CP}$=$\frac{BP}{CE}$,
即:$\frac{8}{14-x}$=$\frac{x}{3}$,
解得x1=12,x2=2,经检验,都符合题意
故BP=12或BP=2.
点评 此题考查了相似三角形的判定与性质以及等腰梯形的性质.注意掌握方程思想的应用是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.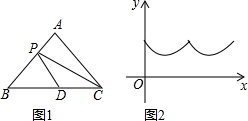 如图1,在△ABC 中,AB=AC,点D是BC的中点,点P沿B→A→C方向从点B运动到点C.设点P经过的路径长为x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
如图1,在△ABC 中,AB=AC,点D是BC的中点,点P沿B→A→C方向从点B运动到点C.设点P经过的路径长为x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
 如图1,在△ABC 中,AB=AC,点D是BC的中点,点P沿B→A→C方向从点B运动到点C.设点P经过的路径长为x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
如图1,在△ABC 中,AB=AC,点D是BC的中点,点P沿B→A→C方向从点B运动到点C.设点P经过的路径长为x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )| A. | BP | B. | AP | C. | DP | D. | CP |
6.在△ABC中,AB=AC,AB的垂直平分线与AC所在直线相交所得的锐角为40°,则底角∠B的大小为多少度?( )
| A. | 20° | B. | 60°或20° | C. | 65°或25° | D. | 60° |
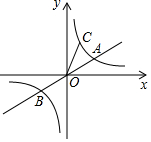 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为4,双曲线y=$\frac{k}{x}$(k>0)上一点C的纵坐标为8,则点B的坐标为(-4,-2),△AOC的面积为15.
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为4,双曲线y=$\frac{k}{x}$(k>0)上一点C的纵坐标为8,则点B的坐标为(-4,-2),△AOC的面积为15. 如图,△ABC中,AB=AC.
如图,△ABC中,AB=AC. 如图,一农户要建一个矩形猪舍,猪舍的一边利用现有的住房墙,另外三边用25m长得建筑材料围成,为方便进出,在垂直于住房墙的一边留一个小门.
如图,一农户要建一个矩形猪舍,猪舍的一边利用现有的住房墙,另外三边用25m长得建筑材料围成,为方便进出,在垂直于住房墙的一边留一个小门.