题目内容
2.先化简再求值:1-$\frac{a-1}{a}$÷$\frac{{a}^{2}-1}{{a}^{2}+2a}$,其中a为不等式-1≤a≤2的整数解.分析 原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算得到最简结果,把a的值代入计算即可求出值.
解答 解:原式=1-$\frac{a-1}{a}$•$\frac{a(a+2)}{(a+1)(a-1)}$=1-$\frac{a+2}{a+1}$=$\frac{a+1-a-2}{a+1}$=-$\frac{1}{a+1}$,
由a为不等式-1≤a≤2的整数解,得到a=-1,0,1,2,
则当a=2时,原式=-$\frac{1}{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
11.若满足方程组$\left\{\begin{array}{l}{3x+2y=2a+1}\\{2x+3y=a-1}\end{array}\right.$的x-y的值是2,则a的值是( )
| A. | 2 | B. | 4 | C. | 0 | D. | 不确定 |
12.下列方程组中,属于二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x+y=5}\\{\frac{1}{x}+\frac{1}{y}=\frac{5}{6}}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{{x}^{2}+y=10}\\{x+y=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=8}\\{xy=-5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{x+y=-3}\end{array}\right.$ |
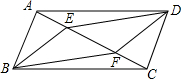 如图,E、F是?ABCD对角线AC上的两点,且BE∥DF,求证:BF=DE.
如图,E、F是?ABCD对角线AC上的两点,且BE∥DF,求证:BF=DE.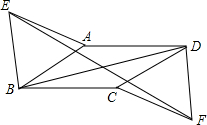 如图,在?ABCD中,分别以AB、CD为边向外作等边△ABE和等边△CDF,
如图,在?ABCD中,分别以AB、CD为边向外作等边△ABE和等边△CDF,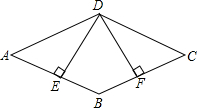 如图,四边形ABCD是平行四边形,DE⊥BC,垂足分别是E,F,且DE=FD.
如图,四边形ABCD是平行四边形,DE⊥BC,垂足分别是E,F,且DE=FD.