题目内容
7.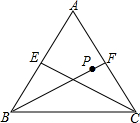 如图,在正△ABC中,CE、BF分别是边AB、AC上的中线,点P是BF上的一动点,若AB=6,则AP+PE的最小值为3$\sqrt{3}$.
如图,在正△ABC中,CE、BF分别是边AB、AC上的中线,点P是BF上的一动点,若AB=6,则AP+PE的最小值为3$\sqrt{3}$.
分析 根据等边三角形的性质得到BF⊥AC,CE⊥AB,推出点A,C关于BF对称,于是得到BF,CE的交点即为点P,CE=AP+PE的最小值,解直角三角形即可得到结论.
解答 解:∵△ABC是等边三角形,CE、BF分别是边AB、AC上的中线,
∴BF⊥AC,CE⊥AB,
∴点A,C关于BF对称,
∴BF,CE的交点即为点P,CE=AP+PE的最小值,
∵∠A=60°AC=6,
∴CE=$\frac{\sqrt{3}}{2}$AC=3$\sqrt{3}$.
故答案为:3$\sqrt{3}$.
点评 此题考查了轴对称-线路最短的问题,确定动点P何位置时,知道PC+PD的值最小是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.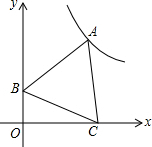 如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )
如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )
 如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )
如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )| A. | (3$\sqrt{3}$,4) | B. | (4,3$\sqrt{3}$) | C. | (4$\sqrt{3}$,3) | D. | (3,4$\sqrt{3}$) |
16.若式子$\frac{\sqrt{x-1}}{x+2}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥1且x≠0 | B. | x>1 且x≠-2 | C. | x≥1 | D. | x≥1 且x≠-2 |
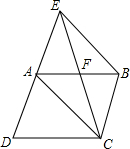 如图,已知E为?ABCD的边DA的延长线上的一点,且AE=AD,EC交AB于点F,那么,EF=CF吗?为什么?
如图,已知E为?ABCD的边DA的延长线上的一点,且AE=AD,EC交AB于点F,那么,EF=CF吗?为什么?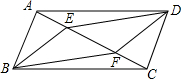 如图,E、F是?ABCD对角线AC上的两点,且BE∥DF,求证:BF=DE.
如图,E、F是?ABCD对角线AC上的两点,且BE∥DF,求证:BF=DE.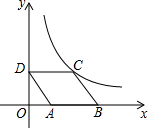 如图,?ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3).反比例函数的图象经过点C,则反比例函数的解析式是y=$\frac{12}{x}$(x≠0).
如图,?ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3).反比例函数的图象经过点C,则反比例函数的解析式是y=$\frac{12}{x}$(x≠0).