题目内容
17.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点A(-2,1),则当x<-1时,函数值y的取值范围是( )| A. | y>2 | B. | -2<y<0 | C. | y>-2 | D. | 0<y<2 |
分析 先根据反比例好图象上点的坐标特征求出k得到反比例函数的解析式为y=-$\frac{2}{x}$,再计算出自变量为-1所对应的函数值,然后根据反比例函数的性质确定x<-1时,函数值y的取值范围.
解答 解:把A(-2,1)代入y=$\frac{k}{x}$得k=-2×1=-2,
所以反比例函数的解析式为y=-$\frac{2}{x}$;
当x=-1时,y=-$\frac{2}{x}$=2,
所以当x<-1时,函数值y的取值范围是0<y<2.
故选D.
点评 本题考查了反比例好图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
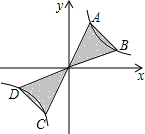 已知反比例函数y=$\frac{3}{x}$上有两点A,B,A点纵坐标是B点纵坐标的3倍,延长AO、BO交曲线的另一支于C,D两点,则图中阴影部分的面积为8.
已知反比例函数y=$\frac{3}{x}$上有两点A,B,A点纵坐标是B点纵坐标的3倍,延长AO、BO交曲线的另一支于C,D两点,则图中阴影部分的面积为8.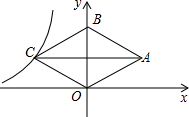 如图,在平面直角坐标系中,菱形OABC的顶点B在y轴正半轴上,菱形的两条对角线的长分别是6和4,函数y=$\frac{k}{x}(x<0)$的图象经过点C,则k的值为-6.
如图,在平面直角坐标系中,菱形OABC的顶点B在y轴正半轴上,菱形的两条对角线的长分别是6和4,函数y=$\frac{k}{x}(x<0)$的图象经过点C,则k的值为-6.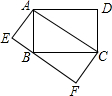 如图,矩形ABCD和矩形AEFC的面积分别为S1,S2,当点B在EF边上时,则S1与S2之间的数量关系为:S1=S2.
如图,矩形ABCD和矩形AEFC的面积分别为S1,S2,当点B在EF边上时,则S1与S2之间的数量关系为:S1=S2.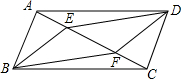 如图,E、F是?ABCD对角线AC上的两点,且BE∥DF,求证:BF=DE.
如图,E、F是?ABCD对角线AC上的两点,且BE∥DF,求证:BF=DE.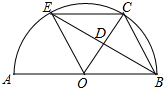 如图,AB是半圆O的直径,点C是半圆O上一点,∠COB=60°,点D是OC的中点,连接BD,BD的延长线交半圆O于点E,连接OE,EC,BC.
如图,AB是半圆O的直径,点C是半圆O上一点,∠COB=60°,点D是OC的中点,连接BD,BD的延长线交半圆O于点E,连接OE,EC,BC.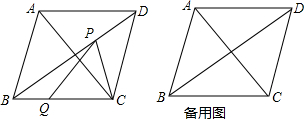 如图,菱形ABCD中,∠ABC<90°,P为该菱形对角线BD上一动点,Q为BC边上一动点,若AC=30,PC+PQ的最小值为24,求菱形ABCD的边长(要求在备用图中画出必要的图形)
如图,菱形ABCD中,∠ABC<90°,P为该菱形对角线BD上一动点,Q为BC边上一动点,若AC=30,PC+PQ的最小值为24,求菱形ABCD的边长(要求在备用图中画出必要的图形)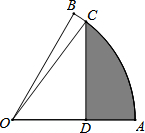 如图,扇形OAB中,∠AOB=60°,扇形半径为3,点C在AB上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为$\frac{9}{8}π-\frac{9}{4}$.
如图,扇形OAB中,∠AOB=60°,扇形半径为3,点C在AB上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为$\frac{9}{8}π-\frac{9}{4}$.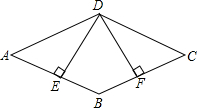 如图,四边形ABCD是平行四边形,DE⊥BC,垂足分别是E,F,且DE=FD.
如图,四边形ABCD是平行四边形,DE⊥BC,垂足分别是E,F,且DE=FD.