Question

12．如图，△ABC中，AB=AC，E、F、G分别是BC、AB、AC上一点，∠FEG=2∠B．
（1）求证：∠BFE=∠AGE；
（2）若$\frac{BE}{CE}$=$\frac{1}{2}$，求$\frac{EF}{EG}$的值．

Answer 1

分析 （1）根据等腰三角形的性质得到∠B=∠C，由三角形的内角和得到∠A+2∠B=180°，等量代换得到∠A+∠FEG=180°，于是得到∠AFE+∠AGE=180°，即可得到结论；
（2）作EM⊥AB于M，EN⊥AC于N，推出△EMB∽△ENC，根据相似三角形的性质得到$\frac{ME}{EN}=\frac{BE}{EC}=\frac{1}{2}$，通过△FME∽△GNE，即可得到结论．

解答 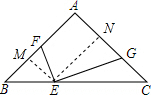解：（1）∵AB=AC，
∴∠B=∠C，
∵∠A+∠B+∠C=180°，
∴∠A+2∠B=180°，
∵∠FEG=2∠B，
∴∠A+∠FEG=180°，
∴∠AFE+∠AGE=180°，
∵∠BFE+∠AFE=180°，
∴∠BFE=∠AGE；

（2）作EM⊥AB于M，EN⊥AC于N，
∵∠B=∠C，∠EMB=∠ENC，
∴△EMB∽△ENC，
∴$\frac{ME}{EN}=\frac{BE}{EC}=\frac{1}{2}$，
∵∠EMF=∠ENG，∠FME=∠GNE，
∴△FME∽△GNE，
∴$\frac{EF}{EG}=\frac{ME}{EN}=\frac{1}{2}$．

点评 本题考查了相似三角形的判定和性质，等腰三角形的性质，三角形的内角和，正确的作出辅助线是解题的关键