题目内容
17.设有点Q(4,0),第一象限内一点P(x,y)在直线y=-x+b上,直线与y轴交于点(0,3),若△OPQ的面积为S,求S与x之间的函数关系式.分析 根据待定系数法求得直线的解析式,然后根据三角形面积公式即可求得.
解答 解:∵直线y=-x+b与y轴交于点(0,3),
∴b=3,
∴y=-x+3,
∵点Q(4,0),
∴OQ=4,
∴S=$\frac{1}{2}$×4(-x+3)=-2x+6,
即S=-2x+6.
点评 本题考查了一次函数图象上点的坐标特征,待定系数法求一次函数的解析式,求得直线的解析式是解题的关键.

练习册系列答案
相关题目
8.关于x的分式方程$\frac{3}{x}$+$\frac{6}{x-1}$-$\frac{x+k}{x(x-1)}$=0有解,则k满足( )
| A. | k≠-3 | B. | k≠5 | C. | k≠-3且k≠-5 | D. | k≠-3且k≠5 |
5.化简分式:$\frac{x-\frac{1}{y}}{y-\frac{1}{x}}$等于( )
| A. | 1 | B. | $\frac{y}{x}$ | C. | $\frac{x}{y}$ | D. | $\frac{x}{y}-\frac{y}{x}$ |
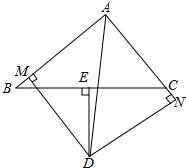 如图,△ABC中,E是BC边上的中点,DE⊥BC于E,交∠BAC的平分线AD于D,过D点作DM⊥AB于M,作DN⊥AC于N,试证明:BM=CN.
如图,△ABC中,E是BC边上的中点,DE⊥BC于E,交∠BAC的平分线AD于D,过D点作DM⊥AB于M,作DN⊥AC于N,试证明:BM=CN. 如图,△ABC中,AB=AC,E、F、G分别是BC、AB、AC上一点,∠FEG=2∠B.
如图,△ABC中,AB=AC,E、F、G分别是BC、AB、AC上一点,∠FEG=2∠B.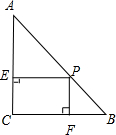 已知△ABC中,AC=BC=3$\sqrt{2}$,∠C=90°,AB上有一动点P,过点P作PE⊥AC于E,PF⊥BC于F.
已知△ABC中,AC=BC=3$\sqrt{2}$,∠C=90°,AB上有一动点P,过点P作PE⊥AC于E,PF⊥BC于F.