题目内容
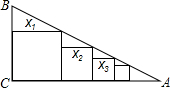已知Rt△ABC中，∠C=90°，BC=1，AC=4，如图把边长分别为x1，x2，x3，…，xn的n个正方形依次放入△ABC中，则第n个正方形的边长xn=考点：相似三角形的判定与性质
专题：规律型
分析：根据正方形的对边平行证明△BDF∽△BCA，然后利用相似三角形对应边成比例列出比例式即可求出第1个正方形的边长，同理利用前两个小正方形上方的三角形相似，根据相似三角形对应边成比例列出比例式即可求出前两个小正方形的边长的关系，以此类推，找出规律便可求出第n个正方形的边长．
解答：解：如下图所示，
∵四边形DCEF是正方形，
∴DF∥CE，
∴△BDF∽△BCA，
∴DF：AC=BD：BC，
即x1：4=（1-x1）：1
解得x1=
，
同理，前两个小正方形上方的三角形相似，
=
解得x2=x12
同理可得，
=
，x3=x1x2=x13
…
以此类推，第n个正方形的边长xn=(
)n．
故答案为：(
)n．
∵四边形DCEF是正方形，
∴DF∥CE，
∴△BDF∽△BCA，
∴DF：AC=BD：BC，
即x1：4=（1-x1）：1
解得x1=
| 4 |
| 5 |
同理，前两个小正方形上方的三角形相似，
| x1 |
| x2 |
| 1-x1 |
| x1-x2 |
解得x2=x12
同理可得，
| x1 |
| x3 |
| 1-x1 |
| x2-x3 |
…
以此类推，第n个正方形的边长xn=(
| 4 |
| 5 |
故答案为：(
| 4 |
| 5 |
点评：本题考查了正方形的性质，相似三角形的判定与性质，解题的关键是根据相似三角形对应边成比例找出后面正方形的边长与第一个正方形的边长的关系．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠C=90°，翻折∠C，使点C落在斜边AB上某一点D处，折痕为EF（点E、F分别在边AC、BC上）．
（1）食品安全是关乎民生的问题，在食品中添加过量的添加剂对人体有害，但适量的添加剂对人体无害且有利于食品的储存和运输，某饮料加工厂生产的A、B两种饮料均需加入同种添加剂，A饮料每瓶需加该添加剂2克，B饮料每瓶需加该添加剂3克，已知270克该添加剂恰好生产了A、B两种饮料共100瓶，问A、B两种饮料各生产了多少瓶？
如图，在△ABC中，AB=2，BC=3.5，∠B=60°，将△ABC绕点A按顺时针旋转一定角度得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为
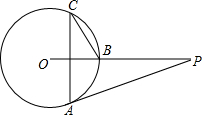如图，P是⊙O外一点，PA是⊙O的切线，A为切点，PO与⊙O相交于 B点，已知∠P=28°，C为⊙O上一点，连接CA，CB，则∠C的度数为（ ）| A、28° | B、62° |
| C、31° | D、56° |