题目内容
已知a+b+c=0且abc≠0,求a(
+
)+b(
+
)+c(
+
)+2的值.
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| 1 |
| c |
| 1 |
| a |
| 1 |
| b |
考点:分式的化简求值
专题:计算题
分析:先算乘法,再根据分式的加法法则进行计算,最后变形后代入,即可求出答案.
解答:解:a(
+
)+b(
+
)+c(
+
)+2
=
+
+
+
+
+
+2
=
+
+
+2
∵a+b+c=0,
∴a+c=-b,a+b=-c,b+c=-a,
∴原式=
+
+
+2=-1-1-1+2=-1.
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| 1 |
| c |
| 1 |
| a |
| 1 |
| b |
=
| a |
| b |
| a |
| c |
| b |
| a |
| b |
| c |
| c |
| a |
| c |
| b |
=
| a+c |
| b |
| a+b |
| c |
| b+c |
| a |
∵a+b+c=0,
∴a+c=-b,a+b=-c,b+c=-a,
∴原式=
| -b |
| b |
| -c |
| c |
| -a |
| a |
点评:本题考查了分式的混合运算和求值的应用,主要考查学生的计算和化简能力,题目比较好,有一定的难度.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 如图,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=
如图,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=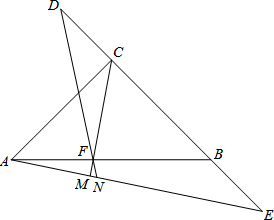 如图,在等腰三角形ABC中,CA=CB,∠ACB=90°,点D、E是直线BC上两点且CD=BE,过点C作CM⊥AE交AE于点M,交AB于点F,连接DF并延长交AE于点N.
如图,在等腰三角形ABC中,CA=CB,∠ACB=90°,点D、E是直线BC上两点且CD=BE,过点C作CM⊥AE交AE于点M,交AB于点F,连接DF并延长交AE于点N. 如图,△ABC中,CF∥AB,
如图,△ABC中,CF∥AB, 如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且∠DBA=∠BCD.
如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且∠DBA=∠BCD.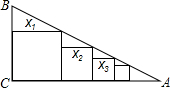 已知Rt△ABC中,∠C=90°,BC=1,AC=4,如图把边长分别为x1,x2,x3,…,xn的n个正方形依次放入△ABC中,则第n个正方形的边长xn=
已知Rt△ABC中,∠C=90°,BC=1,AC=4,如图把边长分别为x1,x2,x3,…,xn的n个正方形依次放入△ABC中,则第n个正方形的边长xn=