题目内容
 (1)食品安全是关乎民生的问题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输,某饮料加工厂生产的A、B两种饮料均需加入同种添加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A、B两种饮料共100瓶,问A、B两种饮料各生产了多少瓶?
(1)食品安全是关乎民生的问题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输,某饮料加工厂生产的A、B两种饮料均需加入同种添加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A、B两种饮料共100瓶,问A、B两种饮料各生产了多少瓶?(2)如图,在平面直角坐标系xOy中,已知一次函数y=kx+b的图象经过点A(1,0),与反比例函数y=
| m |
| x |
①求m的值和一次函数的解析式;
②结合图象直接写出:当x>0时,不等式kx+b>
| m |
| x |
考点:二元一次方程组的应用,一元一次方程的应用,反比例函数与一次函数的交点问题
专题:
分析:(1)设A饮料生产了x瓶,则B饮料生产了(100-x)瓶,根据270克该添加剂恰好生产了A、B两种饮料共100瓶,列方程求解;
(2)①将B点坐标代入,求出m的值,将点A和点B的坐标代入求出k和b的值,继而可求得解析式;
②根据图象,写出解集即可.
(2)①将B点坐标代入,求出m的值,将点A和点B的坐标代入求出k和b的值,继而可求得解析式;
②根据图象,写出解集即可.
解答:解:(1)设A饮料生产了x瓶,则B饮料生产了(100-x)瓶,
由题意得,2x+3(100-x)=270,
解得:x=30,100-x=70,
答:A饮料生产了30瓶,则B饮料生产了70瓶;
(2)①∵反比例函数y=
(x>0)的图象经过点B(2,1),
∴m=1×2=2,
∵一次函数y=kx+b的图象经过点A(1,0),点B(2,1),
∴
,
解得:
,
∴一次函数的解析式为:y=x-1;
②由图象可得:x>2.
由题意得,2x+3(100-x)=270,
解得:x=30,100-x=70,
答:A饮料生产了30瓶,则B饮料生产了70瓶;
(2)①∵反比例函数y=
| m |
| x |
∴m=1×2=2,
∵一次函数y=kx+b的图象经过点A(1,0),点B(2,1),
∴
|
解得:
|
∴一次函数的解析式为:y=x-1;
②由图象可得:x>2.
点评:本题考查了二元一次方程组和反比例函数与一次函数的交点问题,解答本题的关键是读懂题意,找出合适的等量关系,列方程组求解.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
若解分式方程
-
=
产生增根,则m的值是( )
| 2x |
| x+1 |
| m+1 |
| x2+x |
| x+1 |
| x |
| A、-1或-2 | B、-1或2 |
| C、1或2 | D、1或-2 |
 如图,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=
如图,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=
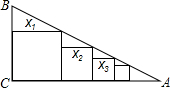 已知Rt△ABC中,∠C=90°,BC=1,AC=4,如图把边长分别为x1,x2,x3,…,xn的n个正方形依次放入△ABC中,则第n个正方形的边长xn=
已知Rt△ABC中,∠C=90°,BC=1,AC=4,如图把边长分别为x1,x2,x3,…,xn的n个正方形依次放入△ABC中,则第n个正方形的边长xn= 如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则
如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则