题目内容
某商场用3400元购进A、B两种新型节能台灯共60盏,这两种台灯的进价、标价如下表.
(1)这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?
| 价格/类型 | A型 | B型 |
| 进价(元/盏) | 40 | 65 |
| 标价(元/盏) | 60 | 100 |
(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?
考点:二元一次方程组的应用,一元一次不等式的应用
专题:
分析:(1)设A型台灯购进x盏,B型台灯购进y盏,根据商场用3400元购进A、B两种新型节能台灯共60盏,列方程组求解;
(2)设购进B型台灯m盏,根据总利润不少于1400元,列不等式求解.
(2)设购进B型台灯m盏,根据总利润不少于1400元,列不等式求解.
解答:解:(1)设A型台灯购进x盏,B型台灯购进y盏,
由题意得,
,
解得:
,
答:A型台灯购进20盏,B型台灯购进40盏;
(2)设购进B型台灯m盏,
由题意得,35m+20(60-m)≥1400,
解得:m≥
.
答:至少需购进B种台灯14盏.
由题意得,
|
解得:
|
答:A型台灯购进20盏,B型台灯购进40盏;
(2)设购进B型台灯m盏,
由题意得,35m+20(60-m)≥1400,
解得:m≥
| 40 |
| 3 |
答:至少需购进B种台灯14盏.
点评:本题考查了二元一次方程组和一元一次不等式的应用,解答本题的关键是读懂题意,找出合适的等量关系和不等关系,列方程和不等式求解.

练习册系列答案
相关题目
2014年4月13日,某中学初三650名学生参加了中考体育测试,为了了解这些学生的体考成绩,现从中抽取了50名学生的体考成绩进行了分析,以下说法正确的是( )
| A、这50名学生是总体的一个样本 |
| B、每位学生的体考成绩是个体 |
| C、50名学生是样本容量 |
| D、650名学生是总体 |
 如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且∠DBA=∠BCD.
如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且∠DBA=∠BCD.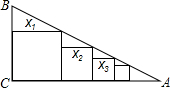 已知Rt△ABC中,∠C=90°,BC=1,AC=4,如图把边长分别为x1,x2,x3,…,xn的n个正方形依次放入△ABC中,则第n个正方形的边长xn=
已知Rt△ABC中,∠C=90°,BC=1,AC=4,如图把边长分别为x1,x2,x3,…,xn的n个正方形依次放入△ABC中,则第n个正方形的边长xn=