题目内容
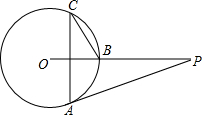 如图,P是⊙O外一点,PA是⊙O的切线,A为切点,PO与⊙O相交于 B点,已知∠P=28°,C为⊙O上一点,连接CA,CB,则∠C的度数为( )
如图,P是⊙O外一点,PA是⊙O的切线,A为切点,PO与⊙O相交于 B点,已知∠P=28°,C为⊙O上一点,连接CA,CB,则∠C的度数为( )| A、28° | B、62° |
| C、31° | D、56° |
考点:切线的性质
专题:
分析:连结AO,求出∠O=180°-90°-28°=62°,再利用圆周角与圆心角的关系求解.
解答:解:如图,连结AO,

∵PA是⊙O的切线,A为切点,
∴∠OAP=90°,
又∵∠P=28°,
∴∠O=180°-90°-28°=62°,
∵∠O和∠C对的同一条弦,
∴∠C=
∠O=
×62°=31°
故答案为:31°.

∵PA是⊙O的切线,A为切点,
∴∠OAP=90°,
又∵∠P=28°,
∴∠O=180°-90°-28°=62°,
∵∠O和∠C对的同一条弦,
∴∠C=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:31°.
点评:本题主要考查了切线的性质及圆周角与圆心角的关系,解决本题的关键是运用圆周角与圆心角的关系来求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2014年4月13日,某中学初三650名学生参加了中考体育测试,为了了解这些学生的体考成绩,现从中抽取了50名学生的体考成绩进行了分析,以下说法正确的是( )
| A、这50名学生是总体的一个样本 |
| B、每位学生的体考成绩是个体 |
| C、50名学生是样本容量 |
| D、650名学生是总体 |
若解分式方程
-
=
产生增根,则m的值是( )
| 2x |
| x+1 |
| m+1 |
| x2+x |
| x+1 |
| x |
| A、-1或-2 | B、-1或2 |
| C、1或2 | D、1或-2 |
分式方程
=
的解是( )
| 4 |
| x+1 |
| 3 |
| x |
| A、x=1 | B、x=-1 |
| C、x=3 | D、x=-3 |
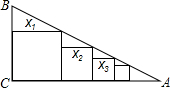 已知Rt△ABC中,∠C=90°,BC=1,AC=4,如图把边长分别为x1,x2,x3,…,xn的n个正方形依次放入△ABC中,则第n个正方形的边长xn=
已知Rt△ABC中,∠C=90°,BC=1,AC=4,如图把边长分别为x1,x2,x3,…,xn的n个正方形依次放入△ABC中,则第n个正方形的边长xn= 如图,在平面直角坐标系中,Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,直角顶点B在x轴上.将Rt△OAB绕点O顺时针旋转90°得到△OCD,边CD与该抛物线交于点P.则DP的长为
如图,在平面直角坐标系中,Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,直角顶点B在x轴上.将Rt△OAB绕点O顺时针旋转90°得到△OCD,边CD与该抛物线交于点P.则DP的长为