题目内容
在平面直角坐标系xOy中,抛物线y=mx2-2x与x轴正半轴交于点A,顶点为B.
(1)求点B的坐标(用含有m的代数式表示)
(2)已知点C(0,2),直线AC与BO交于点D,该抛物线对称轴交于点E,而且△OCD≌△BED,求m的值.
(1)求点B的坐标(用含有m的代数式表示)
(2)已知点C(0,2),直线AC与BO交于点D,该抛物线对称轴交于点E,而且△OCD≌△BED,求m的值.
考点:抛物线与x轴的交点
专题:
分析:(1)利用配方法将一般式化为顶点式,即可求出顶点B的坐标;
(2)设抛物线的对称轴与x轴交于点M.先由ME∥y轴,得出△AME∽△AOC,根据相似三角形对应边的比相等得出
=
=
,于是ME=
OC=1.再根据△OCD≌△BED,得到OC=BE=2,于是BM=BE+ME=3,即-
=-3,进而求出m的值.
(2)设抛物线的对称轴与x轴交于点M.先由ME∥y轴,得出△AME∽△AOC,根据相似三角形对应边的比相等得出
| ME |
| OC |
| AM |
| AO |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| m |
解答: 解:(1)∵y=mx2-2x=m(x-
解:(1)∵y=mx2-2x=m(x-
)2-
,
∴顶点B的坐标为(
,-
);
(2)∵点C(0,-2),
∴OC=2.
设抛物线的对称轴与x轴交于点M.
∵ME∥y轴,
∴△AME∽△AOC,
∴
=
=
,
∴ME=
OC=1.
∵△OCD≌△BED,
∴OC=BE=2,
∴BM=BE+ME=3,
∴-
=-3,
∴m=
.
 解:(1)∵y=mx2-2x=m(x-
解:(1)∵y=mx2-2x=m(x-| 1 |
| m |
| 1 |
| m |
∴顶点B的坐标为(
| 1 |
| m |
| 1 |
| m |
(2)∵点C(0,-2),
∴OC=2.
设抛物线的对称轴与x轴交于点M.
∵ME∥y轴,
∴△AME∽△AOC,
∴
| ME |
| OC |
| AM |
| AO |
| 1 |
| 2 |
∴ME=
| 1 |
| 2 |
∵△OCD≌△BED,
∴OC=BE=2,
∴BM=BE+ME=3,
∴-
| 1 |
| m |
∴m=
| 1 |
| 3 |
点评:考查了抛物线与x轴的交点,其中涉及到抛物线的顶点坐标求法,相似三角形的判定与性质,运用数形结合是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AC=AD,∠C=∠D=90°,那么△ABC与△ABD全等的理由是( )
如图,AC=AD,∠C=∠D=90°,那么△ABC与△ABD全等的理由是( )| A、HL | B、SAS |
| C、ASA | D、AAS |
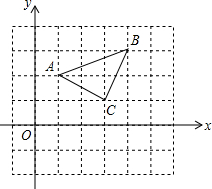 如图所示,△ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).把△A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到△ABC,试写出△A1B1C1三个顶点的坐标.
如图所示,△ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).把△A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到△ABC,试写出△A1B1C1三个顶点的坐标. 一楼房AB后有一假山,其坡面CE与水平地面的夹角为30°,在阳光的照射下,楼房AB落在地上的影长为BC=25米,落在坡面的影长为CE=20米,已知小丽测得同一时刻1米高的竹竿在水平面上的影长为0.8米,求楼房AB的高度.
一楼房AB后有一假山,其坡面CE与水平地面的夹角为30°,在阳光的照射下,楼房AB落在地上的影长为BC=25米,落在坡面的影长为CE=20米,已知小丽测得同一时刻1米高的竹竿在水平面上的影长为0.8米,求楼房AB的高度. 如图已知四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三角形,AB、BC、CD、DA中点分别为P、Q、M、N,求证:四边形PQMN是菱形.
如图已知四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三角形,AB、BC、CD、DA中点分别为P、Q、M、N,求证:四边形PQMN是菱形.