题目内容
 一楼房AB后有一假山,其坡面CE与水平地面的夹角为30°,在阳光的照射下,楼房AB落在地上的影长为BC=25米,落在坡面的影长为CE=20米,已知小丽测得同一时刻1米高的竹竿在水平面上的影长为0.8米,求楼房AB的高度.
一楼房AB后有一假山,其坡面CE与水平地面的夹角为30°,在阳光的照射下,楼房AB落在地上的影长为BC=25米,落在坡面的影长为CE=20米,已知小丽测得同一时刻1米高的竹竿在水平面上的影长为0.8米,求楼房AB的高度.考点:解直角三角形的应用-仰角俯角问题,相似三角形的应用
专题:
分析:过点E作EM⊥AB于点M,可得四边形BNEM为矩形,EN=BM,BN=ME,在Rt△CEN中,根据∠ECN=30°,CE=20米,求出CN、EN的长度,然后根据竹竿在水平面上的影长,可得AM:ME=1:0.8,求出AM的长度,继而可求得AB的长度.
解答:解:过点E作EM⊥AB于点M,
则四边形BNEM为矩形,EN=BM,BN=ME,
在Rt△CEN中,
∵∠ECN=30°,CE=20米,
∴EN=10米,CN=10
米,
∴BM=10米,BN=BC+CN=(25+10
)米,
∵AM:ME=1:0.8,
∴AM=31
+
,
AB=AM+BM=31
+
+10=41
+
.
即楼房AB的高度为(41
+
)米.
则四边形BNEM为矩形,EN=BM,BN=ME,
在Rt△CEN中,
∵∠ECN=30°,CE=20米,
∴EN=10米,CN=10
| 3 |
∴BM=10米,BN=BC+CN=(25+10
| 3 |
∵AM:ME=1:0.8,
∴AM=31
| 1 |
| 4 |
| 25 |
| 2 |
| 3 |
AB=AM+BM=31
| 1 |
| 4 |
| 25 |
| 2 |
| 3 |
| 1 |
| 4 |
| 25 |
| 2 |
| 3 |
即楼房AB的高度为(41
| 1 |
| 4 |
| 25 |
| 2 |
| 3 |
点评:本题考查了解直角三角形的应用,解答本题的关键是根据题目所给的角构造直角三角形,利用三角函数的知识求解.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
下列说法中正确的是( )
A、3x2、-
| ||
| B、单项式2πxy的系数是2 | ||
C、式子
| ||
D、-
|
在△ABC中,点D、E分别在AB、AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
当x=-2
,y=-1
时,代数式x2+y2和代数式-2xy的值分别为M、N,则M、N之间的关系为( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、M<N | B、M=N |
| C、M>N | D、以上三种情况均有可能 |
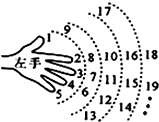 如图为手的示意图,从大拇指开始,按食指,中指,无名指,小指,再回到大拇指的顺序,依次数正整数1,2,3,4,5当数到2014时,对应的手指是( )
如图为手的示意图,从大拇指开始,按食指,中指,无名指,小指,再回到大拇指的顺序,依次数正整数1,2,3,4,5当数到2014时,对应的手指是( )