题目内容
9.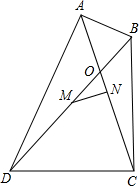 如图,在四边形ABCD中,∠DAB=∠DCB=90°,对角线AC与BD相交于点O,M是BD的中点,MN⊥AC.
如图,在四边形ABCD中,∠DAB=∠DCB=90°,对角线AC与BD相交于点O,M是BD的中点,MN⊥AC.(1)求证:AN=NC;
(2)当MN=3cm,BD=10cm时,求AC的长.
分析 (1)根据直角三角形斜边上的中线等于斜边的一半判定AM=MC=$\frac{1}{2}$BD,从而推知N点是AC边上的中点,所以MN是AC的中垂线;
(2)在Rt△AMN中,利用勾股定理求得AN的长.
解答 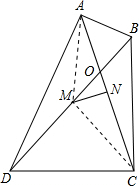 (1)证明:连接AM、MC.
(1)证明:连接AM、MC.
在△DCB和△BAD中,∠DAB=∠DCB=90°,M是边BD的中点,
∴AM=MC=$\frac{1}{2}$BD,
∵MN⊥AC,
∴AN=CN;
(2)解:∵BD=10cm,M、N分别是边BD、AC的中点.
∴AM=$\frac{1}{2}$BD=5cm,
∵MN=3cm,
∴AN=$\sqrt{A{M}^{2}-M{N}^{2}}$=4cm.
点评 本题综合考查了直角三角形斜边上的中线、勾股定理.解题时,通过作辅助线AM、MC构建了直角三角形斜边上的中线,然后利用“直角三角形斜边上的中线等于斜边的一半”来解答问题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 根据所给图形(如图)填空.
根据所给图形(如图)填空. 如图,点A、B、C、D都在⊙O上,OC⊥AB,∠ADC=30°,试探究:四边形AOBC是何种特殊四边形,并给予证明.
如图,点A、B、C、D都在⊙O上,OC⊥AB,∠ADC=30°,试探究:四边形AOBC是何种特殊四边形,并给予证明. 如图.在平行四边形ABCD中,AE∥CF,求证:BE=DF.
如图.在平行四边形ABCD中,AE∥CF,求证:BE=DF. 如图,AB,AC是⊙O的切线,B,C为切点,已知∠BAO=30°,BC=4cm,求⊙O的半径.
如图,AB,AC是⊙O的切线,B,C为切点,已知∠BAO=30°,BC=4cm,求⊙O的半径.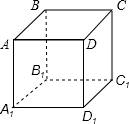 如图所示,有一放在桌面上的正方体的盒子ABCD-A1B1C1D1,在盒子外的顶点A处有一只蚂蚁,而在对角的顶点C1处有一滴蜜糖,蚂蚁应沿着正方体表面什么路径爬行,才能最快吃到蜜糖.请画出正方体的展开图及蚂蚁爬行的路线.
如图所示,有一放在桌面上的正方体的盒子ABCD-A1B1C1D1,在盒子外的顶点A处有一只蚂蚁,而在对角的顶点C1处有一滴蜜糖,蚂蚁应沿着正方体表面什么路径爬行,才能最快吃到蜜糖.请画出正方体的展开图及蚂蚁爬行的路线.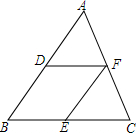 如图,DF、EF是△ABC的两条中位线.我们探究的问题是:这两条中位线和三角形的两条边所围成的四边形的形状与原三角形的边或角有什么关系.建议按下列步骤探索:
如图,DF、EF是△ABC的两条中位线.我们探究的问题是:这两条中位线和三角形的两条边所围成的四边形的形状与原三角形的边或角有什么关系.建议按下列步骤探索: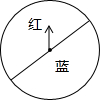 如图是一个红,蓝两色各占一半的转盘,小李与小明做“配紫色”的游戏.规则是:两人各让转盘自由转动一次.当转盘停止转动时.如果指针所在区域的颜色配成紫色.小明胜:如果指针所在区域的颜色配不成紫色.小李胜.在这个游戏中.小李与小明获胜的概率分别是多少?该游戏规则对双方公平吗?为什么?
如图是一个红,蓝两色各占一半的转盘,小李与小明做“配紫色”的游戏.规则是:两人各让转盘自由转动一次.当转盘停止转动时.如果指针所在区域的颜色配成紫色.小明胜:如果指针所在区域的颜色配不成紫色.小李胜.在这个游戏中.小李与小明获胜的概率分别是多少?该游戏规则对双方公平吗?为什么?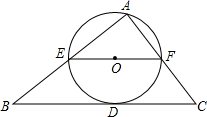 如图,⊙O过点A且与△ABC的边BC相切于D,与AB、AC分别交于E、F,EF经过圆心O,且EF∥BC,若EF=10,BD=12,求BE的长.
如图,⊙O过点A且与△ABC的边BC相切于D,与AB、AC分别交于E、F,EF经过圆心O,且EF∥BC,若EF=10,BD=12,求BE的长.