题目内容
20．
如图，点A、B、C、D都在⊙O上，OC⊥AB，∠ADC=30°，试探究：四边形AOBC是何种特殊四边形，并给予证明．
分析 根据垂径定理得出$\widehat{AC=\widehat{BC}}$，再利用圆周角定理得出∠BOC=60°，再根据等边三角形的判定得出BC=BO=CO，进而得出AO=BO=AC=BC，即可证明结论．
解答 解：∵点A、B、C、D都在⊙O上，OC⊥AB，
∴$\widehat{AC}$=$\widehat{BC}$，
∵∠ADC=30°，
∴∠AOC=∠BOC=2∠ADC=60°，
∴∠BOC的度数为60°，
∵$\widehat{AC=\widehat{BC}}$，
∴AC=BC，
∵AO=BO，
∵∠BOC的度数为60°，BO=CO
∴△BOC为等边三角形，
∴BC=BO=CO，
∴AO=BO=AC=BC，
∴四边形AOBC是菱形．
点评 此题主要考查了菱形的判定以及垂径定理和圆周角定理等知识，根据垂径定理得出$\widehat{AC=\widehat{BC}}$是解决问题的关键．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
10．已知函数y=2x-1中，若x=a时的函数值为1，则a的值是（ ）
| A． | -1 | B． | 1 | C． | -3 | D． | 3 |
如图，在梯形ABCD中，AD∥BC，AD=3，BC=9，AB=6，CD=4．若EF∥BC，且梯形AEFD与梯形EBCF的周长相等，则EF的长为$\frac{39}{5}$．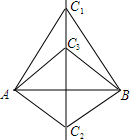
已知：如图，C1A=C1B，C2A=C2B．C3是直线C1C2上一点．求证：C3A=C3B．
已知b是最小的正整数，且a，b满足（c-5）2+|a+b|=0．请回答题：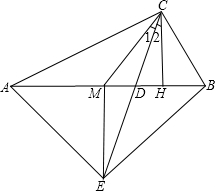
已知：如图，在Rt△ABC中，∠ACB=90°，点M是AB边的中点，CH⊥AB于点H，CD平分∠ACB．
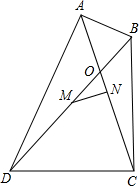如图，在四边形ABCD中，∠DAB=∠DCB=90°，对角线AC与BD相交于点O，M是BD的中点，MN⊥AC．