题目内容
4. 如图,AB,AC是⊙O的切线,B,C为切点,已知∠BAO=30°,BC=4cm,求⊙O的半径.
如图,AB,AC是⊙O的切线,B,C为切点,已知∠BAO=30°,BC=4cm,求⊙O的半径.
分析 连接OB、OC.由切线长定理可知AB=AC,又因为OB=OC,从而可知OA是BC的垂直平分线,故此BD=CD=2,利用特殊锐角三角函数可知AB=4,接下来在Rt△OAB中利用特殊锐角三角函数值可求得BO=$\frac{4\sqrt{3}}{3}$.
解答 解:如图所示:连接OB、OC.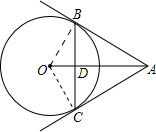
∵AB,AC是⊙O的切线,B,C为切点,
∴AB=AC.
又∵OB=OC,
∴OA是BC的垂直平分线.
∴BD=CD=2,∠BDA=90°.
又∵∠BAO=30°,
∴BD=$\frac{1}{2}AB$.
∴BA=4.
∵AB是圆O的切线,
∴OB⊥BA.
∴BO=ABtan30°=4×$\frac{\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$.
∴圆O的半径为$\frac{4\sqrt{3}}{3}$.
点评 本题主要考查的是切线的性质、线段垂直平分线的判定、特殊锐角三角函数值,掌握本题的辅助线的作法是解题的关键.

练习册系列答案
相关题目
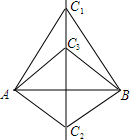 已知:如图,C1A=C1B,C2A=C2B.C3是直线C1C2上一点.求证:C3A=C3B.
已知:如图,C1A=C1B,C2A=C2B.C3是直线C1C2上一点.求证:C3A=C3B.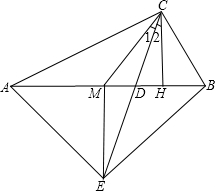 已知:如图,在Rt△ABC中,∠ACB=90°,点M是AB边的中点,CH⊥AB于点H,CD平分∠ACB.
已知:如图,在Rt△ABC中,∠ACB=90°,点M是AB边的中点,CH⊥AB于点H,CD平分∠ACB. 如图,在边长为2cm的正△ABC中,分别以A,B,C点为圆心,1cm长为半径作$\widehat{DE}$、$\widehat{EF}$、$\widehat{FD}$,求阴影部分的面积.
如图,在边长为2cm的正△ABC中,分别以A,B,C点为圆心,1cm长为半径作$\widehat{DE}$、$\widehat{EF}$、$\widehat{FD}$,求阴影部分的面积.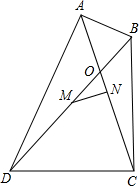 如图,在四边形ABCD中,∠DAB=∠DCB=90°,对角线AC与BD相交于点O,M是BD的中点,MN⊥AC.
如图,在四边形ABCD中,∠DAB=∠DCB=90°,对角线AC与BD相交于点O,M是BD的中点,MN⊥AC. 如图所示,在△ABC中,D、E、F分别为AB、AC、BC的中点,求证:△FED∽△ABC.
如图所示,在△ABC中,D、E、F分别为AB、AC、BC的中点,求证:△FED∽△ABC. 如图,在⊙O中,∠ACB=∠D=60°,AC=4,求△ABC的周长.
如图,在⊙O中,∠ACB=∠D=60°,AC=4,求△ABC的周长.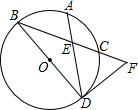 如图,BD是⊙O的直径,点A是劣弧BC的中点,DF是⊙O的切线交BC于点F,AD交BC于点E.
如图,BD是⊙O的直径,点A是劣弧BC的中点,DF是⊙O的切线交BC于点F,AD交BC于点E.