题目内容
19.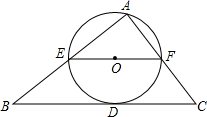 如图,⊙O过点A且与△ABC的边BC相切于D,与AB、AC分别交于E、F,EF经过圆心O,且EF∥BC,若EF=10,BD=12,求BE的长.
如图,⊙O过点A且与△ABC的边BC相切于D,与AB、AC分别交于E、F,EF经过圆心O,且EF∥BC,若EF=10,BD=12,求BE的长.
分析 过点E作EG⊥BC,垂足为G,连接OD,先证明四边形OEGD是正方形,从而可求得BG=7,EG=5,然后由勾股定理可求得BE的长.
解答 解:过点E作EG⊥BC,垂足为G,连接OD.
∵BC与圆O相切,
∴OD⊥BC.
∵EF∥BC,
∴OD⊥EF.
又∵EG⊥BC,OE=OD,
∴四边形OEGD为正方形.
∴BG=7,EG=5.
在Rt△BEG中,由勾股定理得:BE=$\sqrt{{7}^{2}+{5}^{2}}$=$\sqrt{74}$.
点评 本题主要考查的是切线的性质、正方形的判定、勾股定理,证得四边形OEGD为正方形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.某日中午,太姥山风景名胜区气温由早晨的-3℃,上升了8℃,这天中午的气温是( )
| A. | -11℃ | B. | 11℃ | C. | 5℃ | D. | -5℃ |
9.在平面直角坐标系中,点M(-1,3)关于x轴对称的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
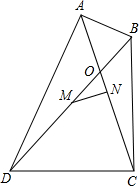 如图,在四边形ABCD中,∠DAB=∠DCB=90°,对角线AC与BD相交于点O,M是BD的中点,MN⊥AC.
如图,在四边形ABCD中,∠DAB=∠DCB=90°,对角线AC与BD相交于点O,M是BD的中点,MN⊥AC. 如图,PA,PB切⊙O于点A,B,点C是优弧$\widehat{AB}$上一点,若∠P=50°,则∠C=65°.
如图,PA,PB切⊙O于点A,B,点C是优弧$\widehat{AB}$上一点,若∠P=50°,则∠C=65°.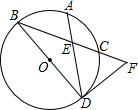 如图,BD是⊙O的直径,点A是劣弧BC的中点,DF是⊙O的切线交BC于点F,AD交BC于点E.
如图,BD是⊙O的直径,点A是劣弧BC的中点,DF是⊙O的切线交BC于点F,AD交BC于点E.