题目内容
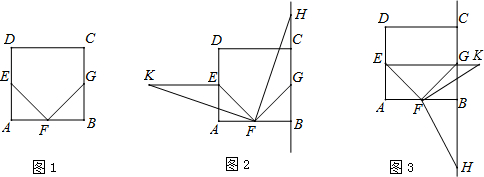
1.在正方形ABCD中,点E、F、G分别是边AD、AB、BC的中点,点H是直线BC上一点,将线段FH绕点F逆时针旋转90°,得到线段FK,连接EK.(1)如图1,求证:EF=FG,且EF⊥FG;
(2)如图2,若点H在线段BC的延长线上,求证:BH=$\frac{\sqrt{2}}{2}$EF+EK;
(3)如图3,若点H在线段BC的反向延长线上,直接写出线段BH、EF、EK之间满足的数量关系为BH=EK-$\frac{\sqrt{2}}{2}$EF.
分析 (1)由正方形的性质得到△AEF≌BGF,再判定出∠EFG=90°即可;
(2)由正方形的性质得到△EFK≌△GFH,再计算出BG=$\frac{\sqrt{2}}{2}$FG,结合图形即可;
(3)由正方形的性质得到△EFK≌△GFH,再计算出BG=$\frac{\sqrt{2}}{2}$FG,结合图形即可;
解答 证明:(1)∵E,F,是正方形ABCD的边AD,AB,BC的中点,
∴AE=AF=FB=BG,∠A=∠B=90°,
∴△AEF≌BGF,
∴EF=FG,∠AFE=∠BFG=45°,
∴∠EFG=180°-∠AFE-∠BFG=90°,
∴EF⊥FG;
(2)由题意有,FH=FK,∠HFK=90°,
∴∠KFE+∠EFH=90°,
∵∠EFG=90°,
∴∠HFG+∠EFH=90°,
∴∠KFE=∠HFG,
∴△EFK≌△GFH,
∴EK=GH,
∵△BFG是等腰直角三角形,
∴BG=$\frac{\sqrt{2}}{2}$FG,
∴BH=BG+GH=$\frac{\sqrt{2}}{2}$FG+EK=$\frac{\sqrt{2}}{2}$EF+EK.
即:BH=$\frac{\sqrt{2}}{2}$EF+EK.
(3)由题意有,FH=FK,∠HFK=90°,
∴∠KFE+∠EFH=90°,
∵∠EFG=90°,
∴∠HFG+∠EFH=90°,
∴∠KFE=∠HFG,
∴△EFK≌△GFH,
∴EK=GH,
∵△BFG是等腰直角三角形,
∴BG=$\frac{\sqrt{2}}{2}$FG,
∴BH=GH-BG=EK-$\frac{\sqrt{2}}{2}$FG=EK-$\frac{\sqrt{2}}{2}$EF.
即:∴BH=EK-$\frac{\sqrt{2}}{2}$EF.
故答案为BH=EK-$\frac{\sqrt{2}}{2}$EF.
点评 此题是四边形的综合题,主要考查了正方形的性质,等腰直角三角形的性质,旋转的性质,解本题的关键是判定三角形全等(如△EFK≌△GFH).

 活力课时同步练习册系列答案
活力课时同步练习册系列答案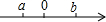 实数a、b在数轴上对应点的位置如图所示:则3a-$\sqrt{(a-b)^{2}}$=4a-b.
实数a、b在数轴上对应点的位置如图所示:则3a-$\sqrt{(a-b)^{2}}$=4a-b.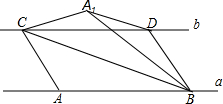 如图,直线a与b平行,点A、B是直线a上两个定点,点CD在直线b上运动(点C在点D的左侧),AB=CD=4cm,a、b之间的距离为$\sqrt{3}$cm,连接AC、BD、BC,把△ABC沿BC折叠得△A1BC.
如图,直线a与b平行,点A、B是直线a上两个定点,点CD在直线b上运动(点C在点D的左侧),AB=CD=4cm,a、b之间的距离为$\sqrt{3}$cm,连接AC、BD、BC,把△ABC沿BC折叠得△A1BC.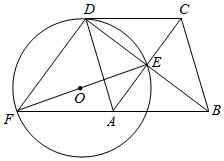 如图,菱形ABCD的对角线AC、BD相交于点E,F是BA延长线上一点,连接EF,以EF为直径作⊙O.
如图,菱形ABCD的对角线AC、BD相交于点E,F是BA延长线上一点,连接EF,以EF为直径作⊙O. 已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论中一定成立的是①②③(把所有正确结论的序号都填在横线上)
已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论中一定成立的是①②③(把所有正确结论的序号都填在横线上) 已知直线l1∥l2,A是l1上一点,B是l2上一点,直线l3和直线l1,l2交于点C和D,在直线CD上有一点P
已知直线l1∥l2,A是l1上一点,B是l2上一点,直线l3和直线l1,l2交于点C和D,在直线CD上有一点P