��Ŀ����
3���Ķ����⣺���ڶ���ʽx2+2ax+a2����ֱ���ù�ʽ���ֽ�Ϊ��x+a��2����ʽ�������ڶ���ʽx2+2ax-3a2���Ͳ���ֱ���ù�ʽ���ˣ����ǿ��Ը��ݶ���ʽ���ص㣬��x2+2ax-3a2���ȼ���һ��a2���ټ�ȥa2���ʹ����ʽ�ӵ�ֵ���䣮����������£�
x2+2ax-3a2=x2+2ax-3a2+a2-a2����һ����
=x2+2ax+a2-a2-3a2���ڶ�����
=��x+a��2-��2a��2����������
=��x+3a����x-a�������IJ���
�����������ϣ��ش��������⣺
��1��������ʽ�ֽ�Ĺ��̣��ӵڶ��������������õ���������ʽ�ֽ�ķ���D
A���ṫ��ʽ�� B��ƽ���ʽ��
C����ȫƽ����ʽ�� D��û����ʽ�ֽ�
��2���ӵ����������IJ��õ�����������ʽ�ֽ�ķ�����ƽ���ʽ��
��3�����������������m2-6mn+8n2��ʽ�ֽ⣮
���� ��1��������ʽ�ֽⶨ���жϼ��ɣ�
��2������ƽ���ʽ���ɵ�֪��
��3�������ɷ�����ԭʽ����n2�Թ�����ȫƽ��ʽ������ƽ���ʽ�ֽ⼴�ɣ�
��� �⣺��1��������ʽ�ֽ�Ķ��壬�ӵڶ�������������û�н��ö���ʽ��Ϊ��ʽ�Ļ�����ʽ��
�ʴӵڶ�����������û����ʽ�ֽ⣻
��2���ӵ����������IJ�������ƽ���ʽ������ʽ��Ϊ����ʽ�Ļ���
���õ�����ʽ�ֽⷽ����ƽ���ʽ����
��3��m2-6mn+8n2��
=m2-6mn+9n2-n2��
=��m-3n��2-n2��
=��m-3n+n����m-3n-n����
=��m-2n����m-4n����
�ʴ�Ϊ����1��D����2��ƽ���ʽ����
���� ���⿼��ʮ����˷��ֽ���ʽ������Ĺؼ���ȷ���ⷶ���ķֽ���̣�Ȼ�����������ʽ����ǡ����������������ù�ʽ���зֽ⣬ʵ����ʮ����˷��ֽ���ʽ��

��ϰ��ϵ�д�
 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�
�����Ŀ
18�������x+a����x+b���Ľ���в���x��һ�����ôa��bӦ���㣨������
| A�� | a=b | B�� | a=0 | C�� | ab=1 | D�� | a+b=0 |
2�����ж���ʽ�У������ù�ʽ���ֽ���ʽ���ǣ�������
| A�� | -a2+b2 | B�� | m2+2mn+2n2 | C�� | x2+4xy+4y2 | D�� | x2-$\frac{1}{2}$xy+$\frac{1}{16}$y2 |
 ��֪��������y=x2+bx+c������A��2��-3����B��4��5����
��֪��������y=x2+bx+c������A��2��-3����B��4��5����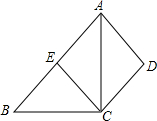 ��ͼ���ı���ABCD�У�AB��CD��ACƽ�֡�BAD��CE��AD��AB��E��
��ͼ���ı���ABCD�У�AB��CD��ACƽ�֡�BAD��CE��AD��AB��E��