题目内容
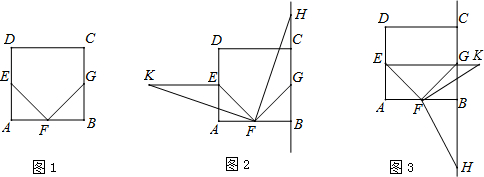
16.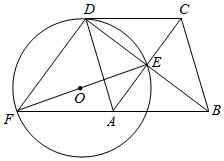 如图,菱形ABCD的对角线AC、BD相交于点E,F是BA延长线上一点,连接EF,以EF为直径作⊙O.
如图,菱形ABCD的对角线AC、BD相交于点E,F是BA延长线上一点,连接EF,以EF为直径作⊙O.(1)求证:AE∥FD;
(2)试判断AF和AB的数量关系,并证明你的结论.
分析 (1)根据圆周角定理可得∠FDE=90°,根据菱形的性质可得∠AEB=90°,即可得到∠AEB=∠FDE,问题得以解决;
(2)由于AB=DC,要证AF=AB,只需证AF=DC,只需证四边形ACDF是平行四边形即可.
解答 解:(1)∵EF是⊙O的直径,
∴∠FDE=90°;
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AEB=90°,
又∵∠FDE=90°,
∴∠AEB=∠FDE,
∴AE∥FD;
(2)AF=AB;
理由如下:
∵四边形ABCD是菱形,
∴AB∥CD,CD=AB,
又∵AC∥DF
∴四边形FACD是平行四边形,
故AF=DC=AB.
点评 本题主要考查了圆周角定理、菱形的性质、平行四边形的判定与性质.

练习册系列答案
相关题目
18.如果(x+a)(x+b)的结果中不含x的一次项,那么a、b应满足( )
| A. | a=b | B. | a=0 | C. | ab=1 | D. | a+b=0 |
5.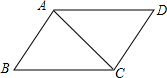 如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )
如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )
 如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )
如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )| A. | SSS | B. | SAS | C. | ASA | D. | HL |
 如图,MN与BC在同一条直线上,且MN=BC=2,点B和点N重合,以MN为底作高为2的等腰△PMN,以BC为边作正方形ABCD,若设△PMN沿射线BC方向平移的距离为x,两图形重合部分的面积为y,则y关于x的函数大致图象是( )
如图,MN与BC在同一条直线上,且MN=BC=2,点B和点N重合,以MN为底作高为2的等腰△PMN,以BC为边作正方形ABCD,若设△PMN沿射线BC方向平移的距离为x,两图形重合部分的面积为y,则y关于x的函数大致图象是( )
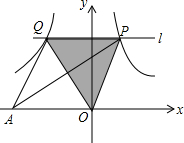 如图,在平面直角坐标系中,直线l∥x轴,且直线l分别与反比例函数y=$\frac{6}{x}$(x>0)和y=-$\frac{8}{x}$(x<0)的图象交于点P、Q,连结PO、QO,则△PAQ的面积为7.
如图,在平面直角坐标系中,直线l∥x轴,且直线l分别与反比例函数y=$\frac{6}{x}$(x>0)和y=-$\frac{8}{x}$(x<0)的图象交于点P、Q,连结PO、QO,则△PAQ的面积为7.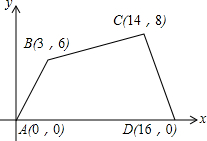 如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),
如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),