题目内容
14.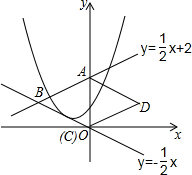 如图,直线y=$\frac{1}{2}x+2$与y轴交于点A,与直线y=-$\frac{1}{2}x$交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x-h)2+k的顶点在直线y=-$\frac{1}{2}x$上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
如图,直线y=$\frac{1}{2}x+2$与y轴交于点A,与直线y=-$\frac{1}{2}x$交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x-h)2+k的顶点在直线y=-$\frac{1}{2}x$上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )| A. | -2$≤h≤\frac{1}{2}$ | B. | -2≤h≤1 | C. | -1$≤h≤\frac{3}{2}$ | D. | -1$≤h≤\frac{1}{2}$ |
分析 将y=$\frac{1}{2}x+2$与y=-$\frac{1}{2}x$联立可求得点B的坐标,然后由抛物线的顶点在直线y=-$\frac{1}{2}x$可求得k=-$\frac{1}{2}h$,于是可得到抛物线的解析式为y=(x-h)2-$\frac{1}{2}$h,由图形可知当抛物线经过点B和点C时抛物线与菱形的边AB、BC均有交点,然后将点C和点B的坐标代入抛物线的解析式可求得h的值,从而可判断出h的取值范围.
解答 解:∵将y=$\frac{1}{2}x+2$与y=-$\frac{1}{2}x$联立得:$\left\{\begin{array}{l}{y=\frac{1}{2}x+2}\\{y=-\frac{1}{2}x}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$.
∴点B的坐标为(-2,1).
由抛物线的解析式可知抛物线的顶点坐标为(h,k).
∵将x=h,y=k,代入得y=-$\frac{1}{2}x$得:-$\frac{1}{2}$h=k,解得k=-$\frac{1}{2}h$,
∴抛物线的解析式为y=(x-h)2-$\frac{1}{2}$h.
如图1所示:当抛物线经过点C时.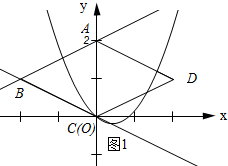
将C(0,0)代入y=(x-h)2-$\frac{1}{2}$h得:h2-$\frac{1}{2}$h=0,解得:h1=0(舍去),h2=$\frac{1}{2}$.
如图2所示:当抛物线经过点B时.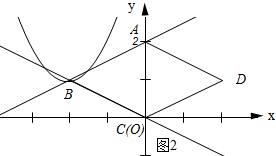
将B(-2,1)代入y=(x-h)2-$\frac{1}{2}$h得:(-2-h)2-$\frac{1}{2}$h=1,整理得:2h2+7h+6=0,解得:h1=-2,h2=-$\frac{3}{2}$(舍去).
综上所述,h的范围是-2≤h≤$\frac{1}{2}$.
故选A.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了一次函数的交点与一元二次方程组的关系、待定系数法求二次函数的解析式,通过平移抛物线探究出抛物线与菱形的边AB、BC均有交点时抛物线经过的“临界点”为点B和点C是解题解题的关键.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
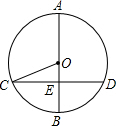 如图,⊙O中直径AB⊥弦CD于E,若AB=26,CD=24,则OE=5.
如图,⊙O中直径AB⊥弦CD于E,若AB=26,CD=24,则OE=5.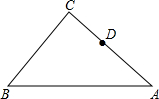 如图,在Rt△ABC中,∠C=90°,AC=14,tanA=$\frac{3}{4}$,点D是边AC上一点,AD=8,点E是边AB上一点,以点E为圆心,EA为半径作圆,经过点D,点F是边AC上一动点(点F不与A、C重合),作FG⊥EF,交射线BC于点G.
如图,在Rt△ABC中,∠C=90°,AC=14,tanA=$\frac{3}{4}$,点D是边AC上一点,AD=8,点E是边AB上一点,以点E为圆心,EA为半径作圆,经过点D,点F是边AC上一动点(点F不与A、C重合),作FG⊥EF,交射线BC于点G.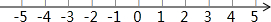 解不等式组$\left\{\begin{array}{l}{3x-2<2x①}\\{\frac{1+x}{2}-1≤x②}\end{array}\right.$请结合题意填空,完成本题的解答.
解不等式组$\left\{\begin{array}{l}{3x-2<2x①}\\{\frac{1+x}{2}-1≤x②}\end{array}\right.$请结合题意填空,完成本题的解答.