题目内容
9.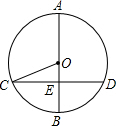 如图,⊙O中直径AB⊥弦CD于E,若AB=26,CD=24,则OE=5.
如图,⊙O中直径AB⊥弦CD于E,若AB=26,CD=24,则OE=5.
分析 先根据垂径定理求出CE的长,再根据勾股定理得出OE的长.
解答 解:∵直径AB⊥弦CD于E,CD=24,
∴CE=$\frac{1}{2}$CD=$\frac{1}{2}$×24=12,
∵AB=26,
∴OC=$\frac{1}{2}$AB=$\frac{1}{2}$×26=13,
∴OE=$\sqrt{O{C}^{2}-C{E}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5.
故答案为:5.
点评 本题考查的是垂径定理及勾股定理,熟知垂直于弦的直径平分弦是解答此题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
4.甲校男生占全校总人数的50%,乙校女生占全校总人数的50%,则甲乙两校女生人数相比( )
| A. | 甲校多于乙校 | B. | 甲校少于乙校 | C. | 甲乙两校一样多 | D. | 不能确定 |
14.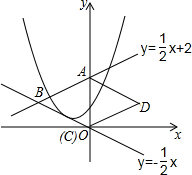 如图,直线y=$\frac{1}{2}x+2$与y轴交于点A,与直线y=-$\frac{1}{2}x$交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x-h)2+k的顶点在直线y=-$\frac{1}{2}x$上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
如图,直线y=$\frac{1}{2}x+2$与y轴交于点A,与直线y=-$\frac{1}{2}x$交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x-h)2+k的顶点在直线y=-$\frac{1}{2}x$上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
 如图,直线y=$\frac{1}{2}x+2$与y轴交于点A,与直线y=-$\frac{1}{2}x$交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x-h)2+k的顶点在直线y=-$\frac{1}{2}x$上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
如图,直线y=$\frac{1}{2}x+2$与y轴交于点A,与直线y=-$\frac{1}{2}x$交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x-h)2+k的顶点在直线y=-$\frac{1}{2}x$上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )| A. | -2$≤h≤\frac{1}{2}$ | B. | -2≤h≤1 | C. | -1$≤h≤\frac{3}{2}$ | D. | -1$≤h≤\frac{1}{2}$ |
18. 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )
 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )| A. | 三棱柱 | B. | 三棱锥 | C. | 四棱柱 | D. | 四棱锥 |

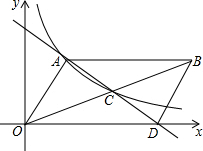 如图,双曲线y=$\frac{k}{x}$(x>0)经过△OAB的顶点A和OB的中点C.AB∥x轴,点A的坐标为(4,6),连接AC交x轴于D.连接BD.
如图,双曲线y=$\frac{k}{x}$(x>0)经过△OAB的顶点A和OB的中点C.AB∥x轴,点A的坐标为(4,6),连接AC交x轴于D.连接BD.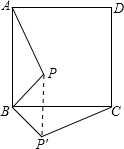 正方形ABCD内一点P,AB=5,BP=2,把△ABP绕点B顺时针旋转90°得到△CBP′,则PP′的长为2$\sqrt{2}$.
正方形ABCD内一点P,AB=5,BP=2,把△ABP绕点B顺时针旋转90°得到△CBP′,则PP′的长为2$\sqrt{2}$.