题目内容
4. 解不等式组$\left\{\begin{array}{l}{3x-2<2x①}\\{\frac{1+x}{2}-1≤x②}\end{array}\right.$请结合题意填空,完成本题的解答.
解不等式组$\left\{\begin{array}{l}{3x-2<2x①}\\{\frac{1+x}{2}-1≤x②}\end{array}\right.$请结合题意填空,完成本题的解答.(Ⅰ)解不等式①,得x<2;
(Ⅱ)解不等式②,得x≥-1;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为-1≤x<2.
分析 分别求出每一个不等式的解集,将不等式的解集表示在数轴上,即可确定不等式组的解集.
解答 解:解不等式①,得:x<2,
解不等式②,得:x≥-1,
把不等式①和②的解集表示在数轴上如下: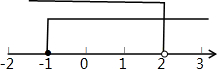
故不等式组的解集为:-1≤x<2,
故答案为:(Ⅰ)x<2;(Ⅱ)x≥-1;(Ⅳ)-1≤x<2.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,正确将不等式解集表示在数轴上是解答此题的关键.

练习册系列答案
相关题目
14.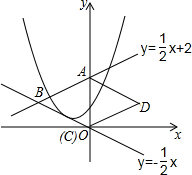 如图,直线y=$\frac{1}{2}x+2$与y轴交于点A,与直线y=-$\frac{1}{2}x$交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x-h)2+k的顶点在直线y=-$\frac{1}{2}x$上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
如图,直线y=$\frac{1}{2}x+2$与y轴交于点A,与直线y=-$\frac{1}{2}x$交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x-h)2+k的顶点在直线y=-$\frac{1}{2}x$上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
 如图,直线y=$\frac{1}{2}x+2$与y轴交于点A,与直线y=-$\frac{1}{2}x$交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x-h)2+k的顶点在直线y=-$\frac{1}{2}x$上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
如图,直线y=$\frac{1}{2}x+2$与y轴交于点A,与直线y=-$\frac{1}{2}x$交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x-h)2+k的顶点在直线y=-$\frac{1}{2}x$上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )| A. | -2$≤h≤\frac{1}{2}$ | B. | -2≤h≤1 | C. | -1$≤h≤\frac{3}{2}$ | D. | -1$≤h≤\frac{1}{2}$ |
12. 如图,AB∥CD,点E在BC上,且CD=CE,∠D=75°,则∠B的度数为( )
如图,AB∥CD,点E在BC上,且CD=CE,∠D=75°,则∠B的度数为( )
 如图,AB∥CD,点E在BC上,且CD=CE,∠D=75°,则∠B的度数为( )
如图,AB∥CD,点E在BC上,且CD=CE,∠D=75°,则∠B的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
16.下列运算正确的是( )
| A. | (a2)3=a5 | B. | 2a-2=$\frac{1}{2{a}^{2}}$ | C. | a6÷a2=a3 | D. | (ab2)2=a2b4 |
13.己知⊙O的半径为$\sqrt{2}$,弦AB=2,以AB为底边,在圆内画⊙0的内接等腰△ABC,则底边AB边上的高CD长为( )
| A. | $\sqrt{2}$+1 | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}+1$或$\sqrt{2}$-1 | D. | $\sqrt{2}$+1或$\sqrt{3}$+1 |