题目内容
15.解方程:$\frac{2x}{{{x^2}+1}}-\frac{{3{x^2}+3}}{2x}+2=0$.分析 因为$\frac{3{x}^{2}+3}{2x}$=3×$\frac{{x}^{2}+1}{2x}$,所以可设$\frac{2x}{{x}^{2}+1}$=y,然后对方程进行整理变形.
解答 解:设y=$\frac{2x}{{x}^{2}+1}$,则原方程化为:y-$\frac{3}{y}$+2=0,
整理,得y2+2y-3=0,
解得:y1=-3,y2=1.
当y1=-3时,$\frac{2x}{{x}^{2}+1}$=-3,得:3x2+2x+3=0,则方程无实数根;
当y2=1时,$\frac{2x}{{x}^{2}+1}$=1,得:x2-2x+1=0,解得x1=x2=1;
经检验x=1是原方程的根,
所以原方程的根为x=1.
点评 此题考查的是换元法解分式方程,用换元法解分式方程,可简化计算过程,减少计算量,是一种常用的方法.要注意总结能用换元法解的分式方程的特点.

练习册系列答案
相关题目
3. 如图,△ABC中AB边的长为10,则△ABC的周长可能为( )
如图,△ABC中AB边的长为10,则△ABC的周长可能为( )
 如图,△ABC中AB边的长为10,则△ABC的周长可能为( )
如图,△ABC中AB边的长为10,则△ABC的周长可能为( )| A. | 16 | B. | 18 | C. | 20 | D. | 22 |
7.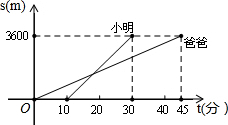 星期天,小明和爸爸去大剧院看电影.爸爸步行先走,小明在爸爸离开家一段时间后骑自行车去,两人按相同的路线前往大剧院,他们所走的路程s(米)和时间t(分)的关系如图所示.则小明追上爸爸时,爸爸共走了( )
星期天,小明和爸爸去大剧院看电影.爸爸步行先走,小明在爸爸离开家一段时间后骑自行车去,两人按相同的路线前往大剧院,他们所走的路程s(米)和时间t(分)的关系如图所示.则小明追上爸爸时,爸爸共走了( )
 星期天,小明和爸爸去大剧院看电影.爸爸步行先走,小明在爸爸离开家一段时间后骑自行车去,两人按相同的路线前往大剧院,他们所走的路程s(米)和时间t(分)的关系如图所示.则小明追上爸爸时,爸爸共走了( )
星期天,小明和爸爸去大剧院看电影.爸爸步行先走,小明在爸爸离开家一段时间后骑自行车去,两人按相同的路线前往大剧院,他们所走的路程s(米)和时间t(分)的关系如图所示.则小明追上爸爸时,爸爸共走了( )| A. | 12分钟 | B. | 15分钟 | C. | 18分钟 | D. | 21分钟 |
5. 如图,已知O是等边△ABC内一点,OD∥BC,OE∥AC,OF∥AB,点D,E,F分别在AB,BC,CA上.若OD:OE:OF=1:2:3,则S四边形ADOF:S四边形BEOD:S四边形CFOE等于( )
如图,已知O是等边△ABC内一点,OD∥BC,OE∥AC,OF∥AB,点D,E,F分别在AB,BC,CA上.若OD:OE:OF=1:2:3,则S四边形ADOF:S四边形BEOD:S四边形CFOE等于( )
 如图,已知O是等边△ABC内一点,OD∥BC,OE∥AC,OF∥AB,点D,E,F分别在AB,BC,CA上.若OD:OE:OF=1:2:3,则S四边形ADOF:S四边形BEOD:S四边形CFOE等于( )
如图,已知O是等边△ABC内一点,OD∥BC,OE∥AC,OF∥AB,点D,E,F分别在AB,BC,CA上.若OD:OE:OF=1:2:3,则S四边形ADOF:S四边形BEOD:S四边形CFOE等于( )| A. | 1:2:3 | B. | 1:4:9 | C. | 7:8:15 | D. | 7:8:21 |