题目内容
4.某中学准备搬迁新校舍,在迁入新校舍之前,同学们就该校学生如何到校问题进行了一次调查,并将调查结果制成了如图所示的两幅不完整的条形统计图和扇形统计图,请你根据图中信息完成下列各题:(1)此次共调查了多少名学生?
(2)扇形统计图中“步行”所在的扇形的圆心角为多少度?
(3)请将条形统计图补充完整.
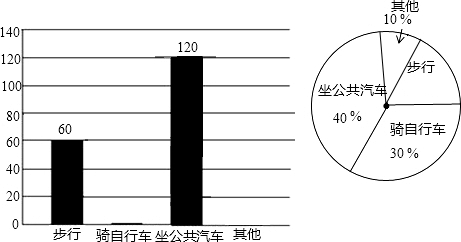
分析 (1)根据坐公共汽车的人数120人占总体的40%进行计算总人数;
(2)利用步行人数除以总人数得出所占的百分比,进一步计算“步行”所在的扇形的圆心角为多少度即可;
(3)计算出骑自行车90人,其他30人,根据(2)中的数据补全统计图即可.
解答 解:(1)120÷40%=300(名);
(2)扇形统计图中“步行”所在的扇形的圆心角为60÷300×360°=72°(或360°×(1-40%-30%-10%)=72°);
(3)骑自行车300×30%=90人,其他300×10%=30人,条形统计图补充如下:
点评 此题考查扇形统计图与条形统计图,需要把统计表和两个统计图相结合,找出统计图中各部分表示项目,从而解决问题.

练习册系列答案
相关题目
14.2014年四川旅游局公布了四川各城市宣传语中英文对照,成华区的宣传口号中有这样一句:“生态城区,现代成华”,它的英文宣传语为“Ecological District,Modem Chenhua”.在路边一块由这个32个英文字母牌拼成的宣传栏上,一只小鸟停留在字母“o”的字母牌上的概率为( )
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{5}{32}$ | D. | $\frac{3}{32}$ |
12.一汽车租赁公司拥有某种型号的汽车50辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数y(辆)有如下关系:
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接判断每月租出的车辆数y(辆)与每辆车的月租金x(元)之间满足三类函数关系中的哪类函数关系,并求出y与x之间的关系式(写出自变量x的取值范围).
(2)已知租出的车每辆每月需要维护费200元,未租出的车每辆每月需要维护费40元.则每月租出的车共需要维护费200(-$\frac{1}{40}$x+300)元(用含x的代数式表示,不必化简),每月未租出的车共需要维护费40[50-(-$\frac{1}{40}$x+300)]元(用含x的代数式表示,不必化简).现设该租赁公司每月扣除所有车辆的维护费后获得的月收益为W元,若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得的月收益W最大?并求出公司的最大月收益是多少元.
| x | … | 10800 | 11000 | 11200 | 11400 | … |
| y | … | 30 | 25 | 20 | 15 | … |
(2)已知租出的车每辆每月需要维护费200元,未租出的车每辆每月需要维护费40元.则每月租出的车共需要维护费200(-$\frac{1}{40}$x+300)元(用含x的代数式表示,不必化简),每月未租出的车共需要维护费40[50-(-$\frac{1}{40}$x+300)]元(用含x的代数式表示,不必化简).现设该租赁公司每月扣除所有车辆的维护费后获得的月收益为W元,若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得的月收益W最大?并求出公司的最大月收益是多少元.
19.已知-3是关于x的方程2x-a=1的解,则a的值是( )
| A. | -7 | B. | -5 | C. | 7 | D. | 5 |
16.甲、乙两名同学从学校出发到科技园去,甲每小时走4km,乙每小时走6km,甲出发1小时后,乙才出发,结果乙比甲早到20分钟,若设学校到科技园的距离为skm,则以下方程正确的是( )
| A. | $\frac{s}{4}+1=\frac{s}{6}$-20 | B. | $\frac{s}{4}+1=\frac{s}{6}-\frac{20}{60}$ | C. | $\frac{s}{4}-1=\frac{s}{6}-\frac{20}{60}$ | D. | $\frac{s}{4}-1=\frac{s}{6}+\frac{20}{60}$ |
 如图,⊙O是△ABC的外接圆,已知∠ABO=35°,则∠ACB=55度.
如图,⊙O是△ABC的外接圆,已知∠ABO=35°,则∠ACB=55度.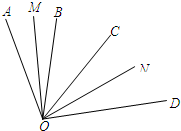 如图,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD.
如图,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD. 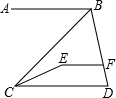 如图,已知AB∥CD,AB∥EF.
如图,已知AB∥CD,AB∥EF.