题目内容
20. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分图形的面积为$\frac{8π}{3}$.
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分图形的面积为$\frac{8π}{3}$.
分析 根据垂径定理求得CE=ED=2$\sqrt{3}$,然后由圆周角定理知∠COE=60°,然后通过解直角三角形求得线段OC、OE的长度,最后将相关线段的长度代入S阴影=S扇形OCB-S△COE+S△BED.
解答 解:如图,假设线段CD、AB交于点E,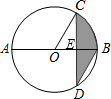
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=ED=2$\sqrt{3}$,
又∵∠CDB=30°,
∴∠COE=2∠CDB=60°,∠OCE=30°,
∴OE=CE•cot60°=2$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=2,OC=2OE=4,
∴S阴影=S扇形OCB-S△COE+S△BED=$\frac{60π×O{C}^{2}}{360}$-$\frac{1}{2}$OE×EC+$\frac{1}{2}$BE•ED=$\frac{8π}{3}$-2$\sqrt{3}$+2$\sqrt{3}$=$\frac{8π}{3}$.
故答案为:$\frac{8}{3}π$.
点评 考查了垂径定理、扇形面积的计算,通过解直角三角形得到相关线段的长度是解答本题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
5.某购物中心一月份的营业额为100万元,三月份的营业额为121万元,设每月的平均增长率为x,则可列方程为( )
| A. | 121(1-x)2=100 | B. | 121(1+x)2=100 | C. | 100(1-x)2=121 | D. | 100(1+x)2=121 |
12.一汽车租赁公司拥有某种型号的汽车50辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数y(辆)有如下关系:
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接判断每月租出的车辆数y(辆)与每辆车的月租金x(元)之间满足三类函数关系中的哪类函数关系,并求出y与x之间的关系式(写出自变量x的取值范围).
(2)已知租出的车每辆每月需要维护费200元,未租出的车每辆每月需要维护费40元.则每月租出的车共需要维护费200(-$\frac{1}{40}$x+300)元(用含x的代数式表示,不必化简),每月未租出的车共需要维护费40[50-(-$\frac{1}{40}$x+300)]元(用含x的代数式表示,不必化简).现设该租赁公司每月扣除所有车辆的维护费后获得的月收益为W元,若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得的月收益W最大?并求出公司的最大月收益是多少元.
| x | … | 10800 | 11000 | 11200 | 11400 | … |
| y | … | 30 | 25 | 20 | 15 | … |
(2)已知租出的车每辆每月需要维护费200元,未租出的车每辆每月需要维护费40元.则每月租出的车共需要维护费200(-$\frac{1}{40}$x+300)元(用含x的代数式表示,不必化简),每月未租出的车共需要维护费40[50-(-$\frac{1}{40}$x+300)]元(用含x的代数式表示,不必化简).现设该租赁公司每月扣除所有车辆的维护费后获得的月收益为W元,若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得的月收益W最大?并求出公司的最大月收益是多少元.
10.小林在某商店购买商品A,B共三次,第一、两次均按标价购物,第三次购物时,商品A,B同时打6折,三次购物商品A,B的数量和费用如下表:
(1)求出商品A,B的标价;
(2)求第三次购物时的总费用是多少?
| 购买商品A的数量(个) | 购买商品B的数量(个) | 购买总费用(元) | |
| 第一次购物 | 6 | 5 | 1140 |
| 第二次购物 | 3 | 7 | 1110 |
| 第三次购物 | 9 | 8 |
(2)求第三次购物时的总费用是多少?
 如图,⊙O是△ABC的外接圆,已知∠ABO=35°,则∠ACB=55度.
如图,⊙O是△ABC的外接圆,已知∠ABO=35°,则∠ACB=55度.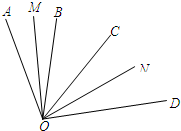 如图,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD.
如图,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD.