题目内容
19. 如图:在△ABC中,∠ACB=90°,AC=BC,⊙O与AB相切,且点0到直线AB的距离等于△ABC中AB边上的高,与边AC,BC分别相交于点M,N,若⊙0半径为2,当⊙0在边AB上滚动时,则$\widehat{MN}$的长为( )
如图:在△ABC中,∠ACB=90°,AC=BC,⊙O与AB相切,且点0到直线AB的距离等于△ABC中AB边上的高,与边AC,BC分别相交于点M,N,若⊙0半径为2,当⊙0在边AB上滚动时,则$\widehat{MN}$的长为( )| A. | $\frac{1}{2}$π | B. | $\frac{\sqrt{3}}{2}$π | C. | π | D. | 无法确定 |
分析 作CD⊥AB垂足为F,点F是切点,LJ OF,OC,作OK⊥AC,OJ⊥BC垂足分别为K、J,先证明△OJC≌△OKH,得OK=OJ再证明RT△OJN≌RT△OKM得到∠NOJ=∠MOK,即可证明∠MON=90°,利用弧长公式求MN的弧长.
解答 解:如图:作CD⊥AB垂足为F,点F是切点,LJ OF,OC,作OK⊥AC,OJ⊥BC垂足分别为K、J.
在△ABC中,∵∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵⊙O与AB相切于点F,且点0到直线AB的距离等于△ABC中AB边上的高
∴OF⊥AB,∵CD⊥AB,
∴OF∥CD,OF=CD,
∴四边形OFDC是平行四边形,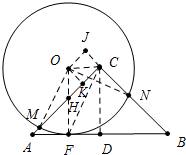
∵∠CDA=90°,
∴四边形OFDC是矩形,
∴OC∥AB,∠COH=90°,
∴∠OCH=∠A=45°,
∴∠OHC=∠OCA=45°,
∴OC=OH,
∵∠OCB=∠OCA+∠ACB=135°,
∴∠OCJ=45°,
在△OJC和△OKH中,
$\left\{\begin{array}{l}{∠J=∠OKC=90°}\\{∠OCJ=∠OHK}\\{OC=OH}\end{array}\right.$,
∴△OJC≌△OKH,
∴OK=OJ,
在RT△OJN和RT△OKM中,
$\left\{\begin{array}{l}{ON=OM}\\{OJ=OK}\end{array}\right.$,
∴△OJN≌△OKM,
∴∠NOJ=∠MOK,
∵∠J=∠OKC=∠JCK=90°,
∴∠JOK=90°,
∵∠NOJ=∠MOK,
∴∠MON=∠JOK=90°
∴$\widehat{MN}$的弧长为=$\frac{1}{4}$•2π•2=π.
故选C.
点评 本题考查圆的有关性质.矩形的判定和性质、全等三角形的判定和性质、弧长公式等知识,添加辅助线构造全等三角形时解题的关键.

| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{5}{32}$ | D. | $\frac{3}{32}$ |
 如图,在⊙O中,直径AB交弦CD于点G,CG=DG,⊙O的切线BE交DO的延长线于点E,F是DE与⊙O的交点,连接BD,BF.
如图,在⊙O中,直径AB交弦CD于点G,CG=DG,⊙O的切线BE交DO的延长线于点E,F是DE与⊙O的交点,连接BD,BF.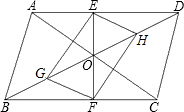 如图,在?ABCD中,对角线AC、BD相交于点O,已知E、F、G、H分别是BC、AD、OB、OD的中点,试说明四边形EGFH是平行四边形.
如图,在?ABCD中,对角线AC、BD相交于点O,已知E、F、G、H分别是BC、AD、OB、OD的中点,试说明四边形EGFH是平行四边形.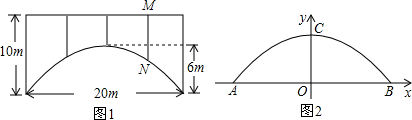
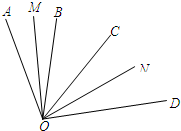 如图,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD.
如图,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD.