Question

8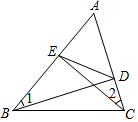．如图，已知在△ABC中，∠ADE=∠ABC，BD，CE交于点O．
（1）求证：AE•AB=AD•AC；
（2）求证：∠1=∠2．

Answer 1

分析 （1）利用有两对角相等的两个三角形相似即可证明△ADE∽△ABC，则该相似三角形的对应边成比例，得证；
（2）欲证明∠1=∠2，只需推知△ABD∽△AEC即可．

解答 证明：（1）∵∠A=∠A，∠ADE=∠ABC，
∴△ADE∽△ABC，
∴$\frac{AE}{AC}$=$\frac{AD}{AB}$，
∴AE•AB=AD•AC；

（2）由（1）知，AE•AB=AD•AC，则$\frac{AD}{AE}$=$\frac{AB}{AC}$．
又∵∠A=∠A，
∴△ABD∽△AEC，
∴∠1=∠2．

点评 本题考查了相似三角形的判定和相似三角形的性质，解题的关键是挖掘出隐藏条件：公共角相等．