题目内容
如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC．将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠PAE．则说明这两个三角形全等的依据是（ ）
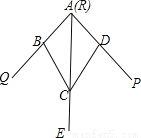
A. SAS B. ASA C. AAS D. SSS
D
【解析】试题解析：在△ADC和△ABC中，
，
∴△ADC≌△ABC（SSS），
∴∠DAC=∠BAC，
即∠QAE=∠PAE．
故选D．
已知ab＞0,|a|=2,|b|=7,则a+b=________．
9或-9
【解析】∵|a|=2,|b|=7,
∴a=±2,b=±7,
∵ab＞0,
∴a、b同号，
∴a=2,b=7或 a=-2,b=-7,
∴a=+b=2+7=9或 a+b=-2-7=-9. 如图，已知∠1=∠2，AC平分∠DAB，试说明AB//DC；
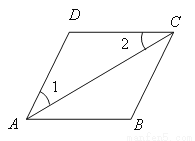
证明见解析
【解析】试题分析：根据角平分线的性质可得,再加上条件,可得,再根据内错角相等两直线平行可得.
证明：∵ AC平分∠DBA（ 已知 ）
∴ ∠1=∠BAC （ 角平分线定义）
又∵∠1=∠2 （ 已知 ）
∴ ∠BAC =∠2 （ 等量代换 ）
∴ AB//DC ( 内错角相等，两直线平行 ) 如图，已知线段AB的垂直平分线CP交AB于点P，且AP=2PC，现欲在线段AB上求作两点D，E，使其满足AD=DC=CE=EB，对于以下甲、乙两种作法：
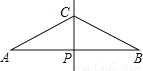
甲：分别作∠ACP、∠BCP的平分线，分别交AB于D、E，则D、E即为所求；乙：分别作AC、BC的垂直平分线，分别交AB于D、E，则D、E两点即为所求．下列说法正确的是（ ）
A. 甲、乙都正确 B. 甲、乙都错误
C. 甲正确，乙错误 D. 甲错误，乙正确
D
【解析】试题解析：甲：虽然CP=AP，
但∠A≠∠ACP，
即∠A≠∠ACD．甲不正确；
乙∵CP是线段AB的中垂线，
∴△ABC是等腰三角形，即AC=BC，∠A=∠B，
作AC、BC之中垂线分别交AB于D、E，
∴∠A=∠ACD，∠B=∠BCE，
∵∠A=∠B，
∴∠A=∠ACD，∠B=∠BCE，
∵AC=BC，
∴△ACD≌... 如图,AB=DC,∠A=∠D.试说明:∠ABC=∠DCB.
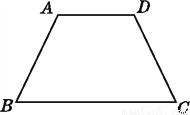
说明见解析.
【解析】试题分析：连接AC、BD，利用“边角边”证明△ABD和△DCA全等，根据全等三角形对应边相等可得AC=BD，再利用“边边边”证明△ABC和△DCB全等，根据全等三角形对应角相等证明即可．
试题解析：证明：如图，连接AC、BD，
在△ABD和△DCA中，
，
∴△ABD≌△DCA（SAS），
∴AC=BD，
在△ABC和△DCB中，
... 如图，将两根钢条AA′，BB′ 的中点O钉在一起，使AA′，BB′ 能绕点O自由转动，就做成一个测量工具，测A′B′ 的长即等于内槽宽AB，那么判定△OAB ≌△OA′B′的理由是（ ）．
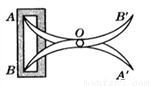
A. 边角边 B. 角边角 C. 边边边 D. 斜边直角边
A
【解析】由题意得边角边可得全等.故选A. 如图，AB∥CD，AD∥BC；则图中的全等三角形共有（ ）
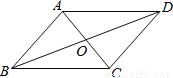
A. 5对 B. 4对 C. 3对 D. 2对
B
【解析】∵AB∥CD，AD∥BC，
∴四边形ABCD为平行四边形，
∴AB=CD，AD=BC，AO=CO，BO=DO，EO=FO，∠DAO=∠BCO，
又∠AOB=∠COD，∠AOD=∠COB，∠AOE=∠COF，
∴△AOB≌△COD（SSS），△AOD≌△COB（SSS），△ABC≌△CDA（SSS），△ABD≌△CDB（SSS）.
故图中的全等三角形共... 若△ABC与△DEF全等,点A和点E,点B和点D分别是对应点,则下列结论错误的是( )
A. BC=EF B. ∠B=∠D
C. ∠C=∠F D. AC=EF
A
【解析】∵点A和点E，点B和点D分别是对应点，
∴△ABC≌△EDF，
∴∠A=∠E，∠B=∠D，∠C=∠F，AC=EF，BC=DF，AB=ED.
故选：A. 如果x2＋ax＋9＝(x＋3)2，那么a的值为( )
A. 3 B. ±3 C. 6 D. ±6
C
【解析】∵x2+ax+9=（x+3）2，而（x+3）2=x2+6x+9；即x2+ax+9=x2