��Ŀ����
��ͼ��AB��CD��AD��BC����ͼ�е�ȫ�������ι��У�������
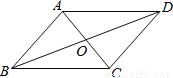
A. 5�� B. 4�� C. 3�� D. 2��
 B
����������AB��CD��AD��BC��
���ı���ABCDΪƽ���ı��Σ�
��AB=CD��AD=BC��AO=CO��BO=DO��EO=FO����DAO=��BCO��
�֡�AOB=��COD����AOD=��COB����AOE=��COF��
���AOB�ա�COD��SSS������AOD�ա�COB��SSS������ABC�ա�CDA��SSS������ABD�ա�CDB��SSS��.
��ͼ�е�ȫ�������ι�...
B
����������AB��CD��AD��BC��
���ı���ABCDΪƽ���ı��Σ�
��AB=CD��AD=BC��AO=CO��BO=DO��EO=FO����DAO=��BCO��
�֡�AOB=��COD����AOD=��COB����AOE=��COF��
���AOB�ա�COD��SSS������AOD�ա�COB��SSS������ABC�ա�CDA��SSS������ABD�ա�CDB��SSS��.
��ͼ�е�ȫ�������ι�...
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д���ͼ����A��������a�������϶�Ӧ�ĵ㣬�����a����a��1�Ĵ�С��ϵ��ʾ��ȷ����(����)
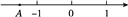
A. a��1����a B. a����a��1 C. 1����a��a D. ��a��a��1
 A
�����������������a�ͩ�a��Ϊ�෴�������ȱ�ʾ��a��λ�ã�Ȼ���ٸ��ݵ����᷽����ʱ���ұߵ����ܱ���ߵ�������бȽϣ�
��������
��ͼ��ʾ��
������ɵã�a��1����a��
��ѡ��A��
A
�����������������a�ͩ�a��Ϊ�෴�������ȱ�ʾ��a��λ�ã�Ȼ���ٸ��ݵ����᷽����ʱ���ұߵ����ܱ���ߵ�������бȽϣ�
��������
��ͼ��ʾ��
������ɵã�a��1����a��
��ѡ��A�� ��ͼ����ABC�У�D��E��AB�ϣ���D��E�ֱ���AC��BC�Ĵ�ֱƽ������һ�㣮
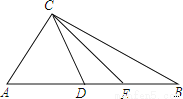
��1������CDE���ܳ�Ϊ4����AB�ij���
��2������ACB=100�㣬���DCE�Ķ�����
��3������ACB=a��90�㣼a��180�㣩�����DCE=___________.
 ��1��4����2��20�㣻��3��2��-180��.
�������������������1�������߶εĴ�ֱƽ���ߵ����ʵõ�DC=DA��EC=EB�����������ε��ܳ���ʽ���㼴�ɣ�
��2�������������ڽǺͶ��������A+��B�Ķ��������ݵ��������ε����������DCA+��ECB������������㼴�ɣ�
��3�����ݣ�2���ķ������
�����������1����D��E�ֱ���AC��BC�Ĵ�ֱƽ������һ�㣬
��DC=...
��1��4����2��20�㣻��3��2��-180��.
�������������������1�������߶εĴ�ֱƽ���ߵ����ʵõ�DC=DA��EC=EB�����������ε��ܳ���ʽ���㼴�ɣ�
��2�������������ڽǺͶ��������A+��B�Ķ��������ݵ��������ε����������DCA+��ECB������������㼴�ɣ�
��3�����ݣ�2���ķ������
�����������1����D��E�ֱ���AC��BC�Ĵ�ֱƽ������һ�㣬
��DC=... ��ͼ��С������һ����ƽ����ABCD������AB=AD��BC=DC���������ϵĵ�A���PRQ�Ķ���R�غϣ�����AB��AD��ʹ���Ƿֱ����ڽǵ������ϣ�����A��C��һ������AE��AE���ǡ�PRQ��ƽ���ߣ��˽�ƽ���ǵĻ�ͼԭ���ǣ����������ṹ���ɵá�ABC�ա�ADC���������С�QAE=��PAE����˵��������������ȫ�ȵ������ǣ�������
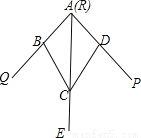
A. SAS B. ASA C. AAS D. SSS
 D
������������������ڡ�ADC�͡�ABC�У�
��
���ADC�ա�ABC��SSS����
���DAC=��BAC��
����QAE=��PAE��
��ѡD��
D
������������������ڡ�ADC�͡�ABC�У�
��
���ADC�ա�ABC��SSS����
���DAC=��BAC��
����QAE=��PAE��
��ѡD�� ��֪����ͼ���ı���ABCD�У�AB=AD��CB=CD��AC��BD���ڵ�E����֤����1����1=��2����2��AC��BD��
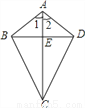
 ��1��֤����������2��֤��������
�������������������1����SSS֤����ABC�ա�ADC���ó���Ӧ����ȼ��ɣ�
��2�����߶δ�ֱƽ���ߵ����ʶ������涨���ó���A��BD�Ĵ�ֱƽ�����ϣ���C��BD�Ĵ�ֱƽ�����ϣ��ó�AC��ֱƽ��BD���ɣ�
�����������1���ڡ�ABC�͡�ADC�У�
��
���ABC�ա�ADC��SSS����
���1=��2��
��2����AB=AD��CB=...
��1��֤����������2��֤��������
�������������������1����SSS֤����ABC�ա�ADC���ó���Ӧ����ȼ��ɣ�
��2�����߶δ�ֱƽ���ߵ����ʶ������涨���ó���A��BD�Ĵ�ֱƽ�����ϣ���C��BD�Ĵ�ֱƽ�����ϣ��ó�AC��ֱƽ��BD���ɣ�
�����������1���ڡ�ABC�͡�ADC�У�
��
���ABC�ա�ADC��SSS����
���1=��2��
��2����AB=AD��CB=... ��ͼ,A,D,E������ͬһֱ����,�ҡ�BAD�ա�ACE,��˵��:
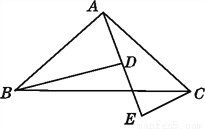
(1)BD=DE+CE;
(2)��ABD����ʲô����ʱ,BD��CE?
 ��1������������2����ADB=90��
�������������������1������ȫ�������ε��������BD=AE��AD=CE������������ɣ�
��2������ȫ�������ε����������E=��BDA=90�㣬�Ƴ���BDE=90�㣬����ƽ���ߵ��ж�������ɣ�
�������: (1)�ߡ�BAD�ա�ACE��
��BD=AE��AD=CE��
��BD=AE=AD+DE=CE+DE��
��BD=DE+CE��
...
��1������������2����ADB=90��
�������������������1������ȫ�������ε��������BD=AE��AD=CE������������ɣ�
��2������ȫ�������ε����������E=��BDA=90�㣬�Ƴ���BDE=90�㣬����ƽ���ߵ��ж�������ɣ�
�������: (1)�ߡ�BAD�ա�ACE��
��BD=AE��AD=CE��
��BD=AE=AD+DE=CE+DE��
��BD=DE+CE��
... ��ͼ,��֪��ABE�ա�ACD,��1=��2,��B=��C,ָ�������Ķ�Ӧ�ߺͶ�Ӧ��.
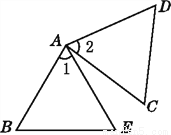
 ������
������������������ȸ��ݡ�ABE�ա�ACD������ȷ����A�Ķ�Ӧ����A����B�Ķ�Ӧ����C����D�Ķ�Ӧ����E��Ȼ����ݶ�Ӧ���㣬���ͼ�μ����ҳ���Ӧ�ߺͶ�Ӧ��.
����������ߡ�ABE�ա�ACD����1=��2����B=��C��
���A�Ķ�Ӧ����A����B�Ķ�Ӧ����C����E�Ķ�Ӧ����D��
���BAE���CAD�Ƕ�Ӧ�ǣ�AB��AC��BE��CD��AD��AE�Ƕ�Ӧ��.
������
������������������ȸ��ݡ�ABE�ա�ACD������ȷ����A�Ķ�Ӧ����A����B�Ķ�Ӧ����C����D�Ķ�Ӧ����E��Ȼ����ݶ�Ӧ���㣬���ͼ�μ����ҳ���Ӧ�ߺͶ�Ӧ��.
����������ߡ�ABE�ա�ACD����1=��2����B=��C��
���A�Ķ�Ӧ����A����B�Ķ�Ӧ����C����E�Ķ�Ӧ����D��
���BAE���CAD�Ƕ�Ӧ�ǣ�AB��AC��BE��CD��AD��AE�Ƕ�Ӧ��. ��ͼ���ڡ�ABC�У�BD�DZ�AC�ϵ����ߣ�E��BC���е㣬����DE.�����BDE�����Ϊ2����ô��ABC�����Ϊ______��
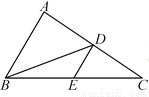
 8
����������E��BC���е�,
�� ,
��BD�DZ�AC�ϵ�����,
�� ,
��,
�֡�BDE�����Ϊ2��
���ABC�����Ϊ8��
�ʴ��ǣ�8.
8
����������E��BC���е�,
�� ,
��BD�DZ�AC�ϵ�����,
�� ,
��,
�֡�BDE�����Ϊ2��
���ABC�����Ϊ8��
�ʴ��ǣ�8. (2x��y)2��(2x��y)2
 16x4��8x2y2��y4
��������������������ݻ��ij˷������㷨���(2x��y)2��(2x��y)2ת��Ϊ��������ƽ���ʽ���㣬��������ȫƽ����ʽ���㼴��.
���������
(2x��y)2��(2x��y)2
=
=
=16x4��8x2y2��y4
16x4��8x2y2��y4
��������������������ݻ��ij˷������㷨���(2x��y)2��(2x��y)2ת��Ϊ��������ƽ���ʽ���㣬��������ȫƽ����ʽ���㼴��.
���������
(2x��y)2��(2x��y)2
=
=
=16x4��8x2y2��y4 
