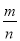题目内容
如图，已知∠1=∠2，AC平分∠DAB，试说明AB//DC；
证明见解析
【解析】试题分析：根据角平分线的性质可得,再加上条件,可得,再根据内错角相等两直线平行可得.
证明：∵ AC平分∠DBA（ 已知 ）
∴ ∠1=∠BAC （ 角平分线定义）
又∵∠1=∠2 （ 已知 ）
∴ ∠BAC =∠2 （ 等量代换 ）
∴ AB//DC ( 内错角相等，两直线平行 )
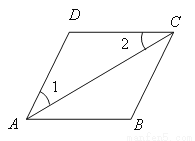
应用题天天练四川大学出版社系列答案某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(如图所示).下表是活动进行中的一组统计数据:
转动转盘 的次数n | 100 | 150 | 200 | 500 | 800 | 1 000 |
落在“铅笔” 区域的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
落在“铅笔” 区域的频率 |
(1)计算并完成表格.
(2)请估计,当n很大时,落在“铅笔”区域的频率将会接近多少?
(3)假如你去转动该转盘一次,你获得哪种奖品的机会大?
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少?
（1）0.68，0.74，0.68，0.69，0.705，0.701；（2）0.7；（3）铅笔；（4）252°.
【解析】分析：（1）根据频率的算法：频率=频数总数可得各个频率，据此填空即可；
（2）、（3）根据频率的定义，可得当n很大时，频率将会接近其概率进行解答；
（4）根据扇形图中，每部分占总体的百分比等于该部分所对应的扇形圆心角的度数与360°的比计算即可.
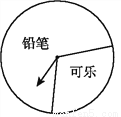
本题解... 如图，若A是有理数a在数轴上对应的点，则关于a，－a，1的大小关系表示正确的是( )
A. a＜1＜－a B. a＜－a＜1 C. 1＜－a＜a D. －a＜a＜1
A
【解析】试题分析：a和﹣a互为相反数，首先表示﹣a的位置，然后再根据当数轴方向朝右时，右边的数总比左边的数大进行比较．
【解析】
如图所示：
由数轴可得：a＜1＜﹣a，
故选：A． 如图,工人师傅在工程施工中需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
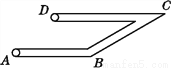
A. AB∥BC B. BC∥CD C. AB∥DC D. AB与CD相交
C
【解析】试题分析：根据同旁内角互补，两直线平行即可求解
本题解析：由∠ABC=150°，∠BCD=30°，得∠ABC+∠BCD=180°，
所以AB∥CD.故选C. 在我们常见的英文字母中,也存在着同位角、内错角、同旁内角,在下面几个字母中,含有内错角最少的字母是( )
A. 
B. 
C. 
D. 
C
【解析】根据内错角的定义可知H中含有2对内错角，M中含有2对内错角；N中含有1对，A中含有2对内错角.
故选：C. 如图，直线a、b与直线c相交，给出下列条件：①∠1＝∠5；②∠4＝∠6；
③∠4＋∠5＝180°；④∠3＋∠8＝180°；其中能判断a//b的是（ ）
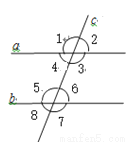
A. ①②③④ B. ①③④ C. ①③ D. ②④
A
【解析】①当∠1=∠5,则a∥b，故此选项正确；
②当∠4=∠6,则a∥b，故此选项正确；
③当∠4+∠5=180°,a∥b，故此选项正确；
④∵∠6=∠8,当∠3+∠8=180°，
∴∠3+∠6=180°，故此选项正确。
故选：A. 如图，△ABC中，D、E在AB上，且D、E分别是AC、BC的垂直平分线上一点．
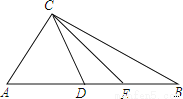
（1）若△CDE的周长为4，求AB的长；
（2）若∠ACB=100°，求∠DCE的度数；
（3）若∠ACB=a（90°＜a＜180°），则∠DCE=___________.
（1）4；（2）20°；（3）2α-180°.
【解析】试题分析：（1）根据线段的垂直平分线的性质得到DC=DA，EC=EB，根据三角形的周长公式计算即可；
（2）根据三角形内角和定理求出∠A+∠B的度数，根据等腰三角形的性质求出∠DCA+∠ECB，根据题意计算即可；
（3）根据（2）的方法解答．
试题解析：（1）∵D、E分别是AC、BC的垂直平分线上一点，
∴DC=... 如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC．将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠PAE．则说明这两个三角形全等的依据是（ ）
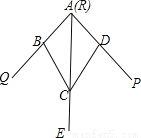
A. SAS B. ASA C. AAS D. SSS
D
【解析】试题解析：在△ADC和△ABC中，
，
∴△ADC≌△ABC（SSS），
∴∠DAC=∠BAC，
即∠QAE=∠PAE．
故选D． 如图，在△ABC中，BD是边AC上的中线，E是BC的中点，连接DE.如果△BDE的面积为2，那么△ABC的面积为______．
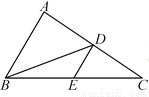
8
【解析】∵E是BC的中点,
∴ ,
∵BD是边AC上的中线,
∴ ,
∴,
又△BDE的面积为2，
∴△ABC的面积为8；
故答案是：8.