��Ŀ����
��ͼ,AB=DC,��A=��D.��˵��:��ABC=��DCB.
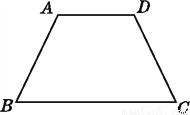
 ˵��������.
���������������������AC��BD�����á��߽DZߡ�֤����ABD�͡�DCAȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�AC=BD�������á��߱߱ߡ�֤����ABC�͡�DCBȫ�ȣ�����ȫ�������ζ�Ӧ�����֤�����ɣ�
���������֤������ͼ������AC��BD��
�ڡ�ABD�͡�DCA�У�
��
���ABD�ա�DCA��SAS����
��AC=BD��
�ڡ�ABC�͡�DCB�У�
...
˵��������.
���������������������AC��BD�����á��߽DZߡ�֤����ABD�͡�DCAȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�AC=BD�������á��߱߱ߡ�֤����ABC�͡�DCBȫ�ȣ�����ȫ�������ζ�Ӧ�����֤�����ɣ�
���������֤������ͼ������AC��BD��
�ڡ�ABD�͡�DCA�У�
��
���ABD�ա�DCA��SAS����
��AC=BD��
�ڡ�ABC�͡�DCB�У�
...
��8�֣����A=2x2+3kx��2x��1��B=��x2+kx��1����3A+6B��ֵ��x��ȡֵ�أ���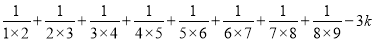 ��ֵ��
��ֵ��
 �������������������A��B����3A+6B����3A+6B��ֵ��x��ȡֵ�ؿ����k��ֵ����k�������ʽ���м��㼴�ɣ�ע������ ��ʽ�ӻ���
��������
3A+6B=3��2x2+3kx��2x��1��+6����x2+kx��1��
=6x 2+9xk-6x-3-6x 2+6xk-6
=15xk-6x-9
=��15k-6��x-9 ,
��3A+6B��ֵ��x��ȡֵ�أ�
��15k=...
�������������������A��B����3A+6B����3A+6B��ֵ��x��ȡֵ�ؿ����k��ֵ����k�������ʽ���м��㼴�ɣ�ע������ ��ʽ�ӻ���
��������
3A+6B=3��2x2+3kx��2x��1��+6����x2+kx��1��
=6x 2+9xk-6x-3-6x 2+6xk-6
=15xk-6x-9
=��15k-6��x-9 ,
��3A+6B��ֵ��x��ȡֵ�أ�
��15k=... �����dz�����Ӣ����ĸ��,Ҳ������ͬλ�ǡ��ڴ��ǡ�ͬ���ڽ�,�����漸����ĸ��,�����ڴ������ٵ���ĸ��(����)
A.  B.
B.  C.
C.  D.
D. 
 C
�������������ڴ��ǵĶ����֪H�к���2���ڴ��ǣ�M�к���2���ڴ��ǣ�N�к���1�ԣ�A�к���2���ڴ���.
��ѡ��C.
C
�������������ڴ��ǵĶ����֪H�к���2���ڴ��ǣ�M�к���2���ڴ��ǣ�N�к���1�ԣ�A�к���2���ڴ���.
��ѡ��C. ��ͼ����ABC�У�D��E��AB�ϣ���D��E�ֱ���AC��BC�Ĵ�ֱƽ������һ�㣮
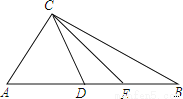
��1������CDE���ܳ�Ϊ4����AB�ij���
��2������ACB=100�㣬���DCE�Ķ�����
��3������ACB=a��90�㣼a��180�㣩�����DCE=___________.
 ��1��4����2��20�㣻��3��2��-180��.
�������������������1�������߶εĴ�ֱƽ���ߵ����ʵõ�DC=DA��EC=EB�����������ε��ܳ���ʽ���㼴�ɣ�
��2�������������ڽǺͶ��������A+��B�Ķ��������ݵ��������ε����������DCA+��ECB������������㼴�ɣ�
��3�����ݣ�2���ķ������
�����������1����D��E�ֱ���AC��BC�Ĵ�ֱƽ������һ�㣬
��DC=...
��1��4����2��20�㣻��3��2��-180��.
�������������������1�������߶εĴ�ֱƽ���ߵ����ʵõ�DC=DA��EC=EB�����������ε��ܳ���ʽ���㼴�ɣ�
��2�������������ڽǺͶ��������A+��B�Ķ��������ݵ��������ε����������DCA+��ECB������������㼴�ɣ�
��3�����ݣ�2���ķ������
�����������1����D��E�ֱ���AC��BC�Ĵ�ֱƽ������һ�㣬
��DC=... ��ͼ���ڡ�ABC�У�DE�DZ�AB�Ĵ�ֱƽ���ߣ�BC=8cm��AC=5cm�����ADC���ܳ�Ϊ��������
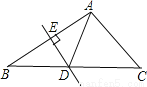
A. 14cm B. 13cm C. 11cm D. 9cm
 B
�������������������DE�DZ�AB�Ĵ�ֱƽ����
��BD=AD
���ADC���ܳ�ΪAC+DC+AD=AC+BC=5+8=13cm��
��ѡB.
B
�������������������DE�DZ�AB�Ĵ�ֱƽ����
��BD=AD
���ADC���ܳ�ΪAC+DC+AD=AC+BC=5+8=13cm��
��ѡB. ��ͼ��С������һ����ƽ����ABCD������AB=AD��BC=DC���������ϵĵ�A���PRQ�Ķ���R�غϣ�����AB��AD��ʹ���Ƿֱ����ڽǵ������ϣ�����A��C��һ������AE��AE���ǡ�PRQ��ƽ���ߣ��˽�ƽ���ǵĻ�ͼԭ���ǣ����������ṹ���ɵá�ABC�ա�ADC���������С�QAE=��PAE����˵��������������ȫ�ȵ������ǣ�������
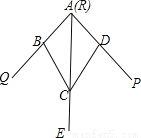
A. SAS B. ASA C. AAS D. SSS
 D
������������������ڡ�ADC�͡�ABC�У�
��
���ADC�ա�ABC��SSS����
���DAC=��BAC��
����QAE=��PAE��
��ѡD��
D
������������������ڡ�ADC�͡�ABC�У�
��
���ADC�ա�ABC��SSS����
���DAC=��BAC��
����QAE=��PAE��
��ѡD�� ��֪����ͼ���ı���ABCD�У�AB=AD��CB=CD��AC��BD���ڵ�E����֤����1����1=��2����2��AC��BD��
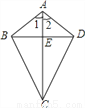
 ��1��֤����������2��֤��������
�������������������1����SSS֤����ABC�ա�ADC���ó���Ӧ����ȼ��ɣ�
��2�����߶δ�ֱƽ���ߵ����ʶ������涨���ó���A��BD�Ĵ�ֱƽ�����ϣ���C��BD�Ĵ�ֱƽ�����ϣ��ó�AC��ֱƽ��BD���ɣ�
�����������1���ڡ�ABC�͡�ADC�У�
��
���ABC�ա�ADC��SSS����
���1=��2��
��2����AB=AD��CB=...
��1��֤����������2��֤��������
�������������������1����SSS֤����ABC�ա�ADC���ó���Ӧ����ȼ��ɣ�
��2�����߶δ�ֱƽ���ߵ����ʶ������涨���ó���A��BD�Ĵ�ֱƽ�����ϣ���C��BD�Ĵ�ֱƽ�����ϣ��ó�AC��ֱƽ��BD���ɣ�
�����������1���ڡ�ABC�͡�ADC�У�
��
���ABC�ա�ADC��SSS����
���1=��2��
��2����AB=AD��CB=... ��ͼ,��֪��ABE�ա�ACD,��1=��2,��B=��C,ָ�������Ķ�Ӧ�ߺͶ�Ӧ��.
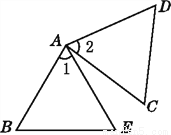
 ������
������������������ȸ��ݡ�ABE�ա�ACD������ȷ����A�Ķ�Ӧ����A����B�Ķ�Ӧ����C����D�Ķ�Ӧ����E��Ȼ����ݶ�Ӧ���㣬���ͼ�μ����ҳ���Ӧ�ߺͶ�Ӧ��.
����������ߡ�ABE�ա�ACD����1=��2����B=��C��
���A�Ķ�Ӧ����A����B�Ķ�Ӧ����C����E�Ķ�Ӧ����D��
���BAE���CAD�Ƕ�Ӧ�ǣ�AB��AC��BE��CD��AD��AE�Ƕ�Ӧ��.
������
������������������ȸ��ݡ�ABE�ա�ACD������ȷ����A�Ķ�Ӧ����A����B�Ķ�Ӧ����C����D�Ķ�Ӧ����E��Ȼ����ݶ�Ӧ���㣬���ͼ�μ����ҳ���Ӧ�ߺͶ�Ӧ��.
����������ߡ�ABE�ա�ACD����1=��2����B=��C��
���A�Ķ�Ӧ����A����B�Ķ�Ӧ����C����E�Ķ�Ӧ����D��
���BAE���CAD�Ƕ�Ӧ�ǣ�AB��AC��BE��CD��AD��AE�Ƕ�Ӧ��. ����ʽ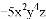 ��ϵ����________�������� _______.
��ϵ����________�������� _______.
 -5 7
������������ʽ�е����������ǵ���ʽ��ϵ����������ĸ��ָ���ĺͽ����������ʽ�Ĵ���.�ɴ˿ɵõ���ʽ��ϵ����-5��������7.
-5 7
������������ʽ�е����������ǵ���ʽ��ϵ����������ĸ��ָ���ĺͽ����������ʽ�Ĵ���.�ɴ˿ɵõ���ʽ��ϵ����-5��������7. 
