题目内容
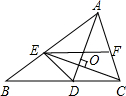 如图,在△ABC中,AD平分∠BAC,CE⊥AD,EF∥BC.求证:EC平分∠FED.
如图,在△ABC中,AD平分∠BAC,CE⊥AD,EF∥BC.求证:EC平分∠FED.考点:全等三角形的判定与性质
专题:
分析:证△AOE≌△AOC,根据全等三角形的性质得出EO=OC,根据平行线得出
=
,推出MO=OD,根据线段垂直平分线性质求出ED=EM,根据等腰三角形的性质得出即可.
| MO |
| OD |
| EO |
| OC |
解答:证明:∵AD平分∠BAC,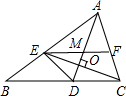
∴∠EAO=∠CAO,
∵CE⊥AD,
∴∠AOE=∠AOC,
∴在△AOE和△AOC中
∴△AOE≌△AOC,
∴EO=OC,
∵EF∥BC,
∴
=
,
∴MO=OD,
∵CE⊥AD,
∴EM=ED,
∴EC平分∠FED.

∴∠EAO=∠CAO,
∵CE⊥AD,
∴∠AOE=∠AOC,
∴在△AOE和△AOC中
|
∴△AOE≌△AOC,
∴EO=OC,
∵EF∥BC,
∴
| MO |
| OD |
| EO |
| OC |
∴MO=OD,
∵CE⊥AD,
∴EM=ED,
∴EC平分∠FED.
点评:本题考查了全等三角形的性质和判定,平行线的性质,等腰三角形的性质,线段垂直平分线性质的应用,主要考查学生的推理能力,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,HL,全等三角形的对应边相等,对应角相等.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
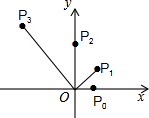 如图,在平面直角坐标系中,已知点P0的坐标为(1,0)将线段OP按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1,又将线段OP1按逆时针方向旋转45°,再将其长度伸长为OP1的2倍得到线段OP2;…;如此进行下去,得到线段OP3,OP4,…OPn(n为正整数)则点P2015的坐标为( )
如图,在平面直角坐标系中,已知点P0的坐标为(1,0)将线段OP按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1,又将线段OP1按逆时针方向旋转45°,再将其长度伸长为OP1的2倍得到线段OP2;…;如此进行下去,得到线段OP3,OP4,…OPn(n为正整数)则点P2015的坐标为( )A、(22014•
| ||||
B、(22012•
| ||||
C、(-22013•
| ||||
| D、(0,-22014) |
已知A(-1,y1),B(1,y2),C(2,y3)三点在抛物线y=x2-2x+m上,则y1、y2、y3的大小关系为( )
| A、y1<y2<y3 |
| B、y3<y2<y1 |
| C、y2<y1<y3 |
| D、y2<y3<y1 |
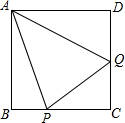 如图,正方形ABCD的边长为1,BC、CD上各有一点P、Q,若∠PAQ=45°,求△CPQ的周长.
如图,正方形ABCD的边长为1,BC、CD上各有一点P、Q,若∠PAQ=45°,求△CPQ的周长. 如图,已知AB=AC,且DC⊥AC,DB⊥AB,求证:AD平分∠CAB.
如图,已知AB=AC,且DC⊥AC,DB⊥AB,求证:AD平分∠CAB.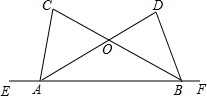 如图,点E、A、B、F在同一条直线上,AD与BC交于点O,已知∠CAE=∠DBF,AC=BD.求证:
如图,点E、A、B、F在同一条直线上,AD与BC交于点O,已知∠CAE=∠DBF,AC=BD.求证: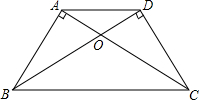 如图,AB⊥AC,DC⊥DB,填空:
如图,AB⊥AC,DC⊥DB,填空: