题目内容
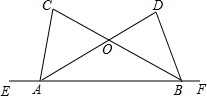 如图,点E、A、B、F在同一条直线上,AD与BC交于点O,已知∠CAE=∠DBF,AC=BD.求证:
如图,点E、A、B、F在同一条直线上,AD与BC交于点O,已知∠CAE=∠DBF,AC=BD.求证:(1)BC=AD;
(2)∠CAD=∠DBC.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)求出∠CAB=∠DBA,根据SAS推出△CAB≌△DBA即可;
(2)根据全等得出∠C=∠D,根据三角形的内角和定理得出即可.
(2)根据全等得出∠C=∠D,根据三角形的内角和定理得出即可.
解答:证明:(1)∵∠CAE=∠DBF,∠CAB+∠CAE=180°,∠DBF+∠DBA=180°,
∴∠CAB=∠DBA,
在△CAB和△DBA中
∴△CAB≌△DBA,
∴BC=AD;
(2)∵△CAB≌△DBA,
∴∠C=∠D,
∵∠COA=∠DOB,∠C+∠CAD+∠COA=180°,∠D+∠DOB+∠DBC=180°,
∴∠CAD=∠DBC.
∴∠CAB=∠DBA,
在△CAB和△DBA中
|
∴△CAB≌△DBA,
∴BC=AD;
(2)∵△CAB≌△DBA,
∴∠C=∠D,
∵∠COA=∠DOB,∠C+∠CAD+∠COA=180°,∠D+∠DOB+∠DBC=180°,
∴∠CAD=∠DBC.
点评:本题考查了全等三角形的性质和判定,三角形内角和定理的应用,解此题的关键是推出△CAB≌△DBA,主要考查学生的推理能力.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
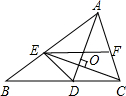 如图,在△ABC中,AD平分∠BAC,CE⊥AD,EF∥BC.求证:EC平分∠FED.
如图,在△ABC中,AD平分∠BAC,CE⊥AD,EF∥BC.求证:EC平分∠FED. 如图,已在AB=AC,AD=AE,∠1=∠2,求证:∠B=∠C.
如图,已在AB=AC,AD=AE,∠1=∠2,求证:∠B=∠C. 已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4,如图所示,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.
已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4,如图所示,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.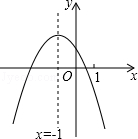 二次函数y=ax2+bx+c (a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c (a≠0)的图象如图,给出下列四个结论: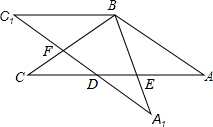 在△ABC中,AB=BC=4,∠ABC=120°,将△ABC绕点B旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
在△ABC中,AB=BC=4,∠ABC=120°,将△ABC绕点B旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.