题目内容
已知A(-1,y1),B(1,y2),C(2,y3)三点在抛物线y=x2-2x+m上,则y1、y2、y3的大小关系为( )
| A、y1<y2<y3 |
| B、y3<y2<y1 |
| C、y2<y1<y3 |
| D、y2<y3<y1 |
考点:二次函数图象上点的坐标特征
专题:计算题
分析:分别计算自变量为-1、1和2所对应的函数值,然后比较函数值的大小即可.
解答:解:当x=-1时,y1=x2-2x+m=1+2+m=3+m;当x=1时,y2=x2-2x+m=1-2+m=-1+m;当x=2时,y3=x2-2x+m=4-4+m=m,
所以y2<y3<y1.
故选D.
所以y2<y3<y1.
故选D.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
相关题目
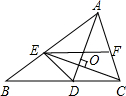 如图,在△ABC中,AD平分∠BAC,CE⊥AD,EF∥BC.求证:EC平分∠FED.
如图,在△ABC中,AD平分∠BAC,CE⊥AD,EF∥BC.求证:EC平分∠FED. 已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4,如图所示,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.
已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4,如图所示,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.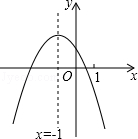 二次函数y=ax2+bx+c (a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c (a≠0)的图象如图,给出下列四个结论: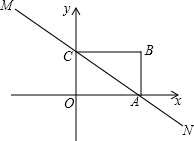 如图,直线MN与x轴,y轴分别相交于A、C两点,分别过A、C两点作x轴,y轴的乘线相交于B点,且OA,OC(OA>OC)的长分别是OC=6,OA=8
如图,直线MN与x轴,y轴分别相交于A、C两点,分别过A、C两点作x轴,y轴的乘线相交于B点,且OA,OC(OA>OC)的长分别是OC=6,OA=8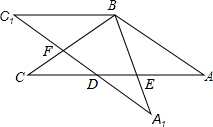 在△ABC中,AB=BC=4,∠ABC=120°,将△ABC绕点B旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
在△ABC中,AB=BC=4,∠ABC=120°,将△ABC绕点B旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.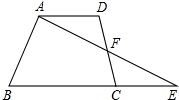 四边形ABCD中,AD∥BC,DF=CF,连接AF并延长交BC延长线于点E.
四边形ABCD中,AD∥BC,DF=CF,连接AF并延长交BC延长线于点E.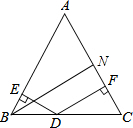 △ABC是等边三角形,点D是BC边上的任意一点,DE⊥AB于点E,DF⊥AC于点F,BN⊥AC于点N,则DE,DF,BN三者的数量关系为
△ABC是等边三角形,点D是BC边上的任意一点,DE⊥AB于点E,DF⊥AC于点F,BN⊥AC于点N,则DE,DF,BN三者的数量关系为