题目内容
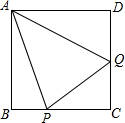 如图,正方形ABCD的边长为1,BC、CD上各有一点P、Q,若∠PAQ=45°,求△CPQ的周长.
如图,正方形ABCD的边长为1,BC、CD上各有一点P、Q,若∠PAQ=45°,求△CPQ的周长.考点:旋转的性质,全等三角形的判定与性质,勾股定理,正方形的性质
专题:
分析:利用旋转的性质以及正方形的性质易得∠PAQ=∠EAP,进而得出△PAQ≌△PAE,则可得出PB+DQ=PE,进而得出答案.
解答: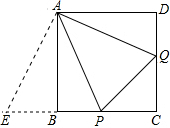 解:将△ADQ旋转到△ABE位置,
解:将△ADQ旋转到△ABE位置,
由旋转可知:△AQD≌△AEB,
∴AQ=AE,BE=DQ,∠DAQ=∠BAE,
∵∠PAQ=45°,∠BAD=90°,
∴∠DAQ+∠BAP=45°,
∴∠BAE+∠BAP=45°,
即:∠EAP=45°,
∴∠PAQ=∠EAP,
在△PAQ和△PAE中,
,
∴△PAQ≌△PAE(SAS),
∴PQ=PE,
∴PQ=PB+DQ,
∴PC+CQ+PQ=BP+DQ+PC+CQ=2AB=2.
即△CPQ的周长为2.
 解:将△ADQ旋转到△ABE位置,
解:将△ADQ旋转到△ABE位置,由旋转可知:△AQD≌△AEB,
∴AQ=AE,BE=DQ,∠DAQ=∠BAE,
∵∠PAQ=45°,∠BAD=90°,
∴∠DAQ+∠BAP=45°,
∴∠BAE+∠BAP=45°,
即:∠EAP=45°,
∴∠PAQ=∠EAP,
在△PAQ和△PAE中,
|
∴△PAQ≌△PAE(SAS),
∴PQ=PE,
∴PQ=PB+DQ,
∴PC+CQ+PQ=BP+DQ+PC+CQ=2AB=2.
即△CPQ的周长为2.
点评:本题考查了旋转的性质以及三角形全等的判定与性质和正方形的性质等知识,根据已知得出PQ=PB+DQ是解题关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
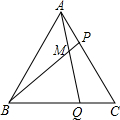 如图,等边三角形ABC中,P、Q两点分别在AC、BC上,AP=CQ,AQ与BP交于点M,求证:∠BMQ=60°.
如图,等边三角形ABC中,P、Q两点分别在AC、BC上,AP=CQ,AQ与BP交于点M,求证:∠BMQ=60°.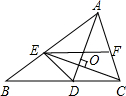 如图,在△ABC中,AD平分∠BAC,CE⊥AD,EF∥BC.求证:EC平分∠FED.
如图,在△ABC中,AD平分∠BAC,CE⊥AD,EF∥BC.求证:EC平分∠FED. 如图,已在AB=AC,AD=AE,∠1=∠2,求证:∠B=∠C.
如图,已在AB=AC,AD=AE,∠1=∠2,求证:∠B=∠C.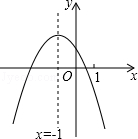 二次函数y=ax2+bx+c (a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c (a≠0)的图象如图,给出下列四个结论: 如图,E、F分别是正方形的边CD、AD上的点,且CE=DF,AE、BF交于点O,下列结论正确的个数为( )
如图,E、F分别是正方形的边CD、AD上的点,且CE=DF,AE、BF交于点O,下列结论正确的个数为( )