题目内容
20.若二次函数y=ax2-2ax+c的图象经过点(-1,0),则方程ax2-2ax+c=0的解为x=-1.分析 二次函数y=ax2-2ax+c的图象经过点(-1,0),则当x=0时,y=0,即ax2-2ax+c=0的解是x=-1,据此求解.
解答 解:∵二次函数y=ax2-2ax+c的图象经过点(-1,0),
∴当x=1时,ax2-2ax+c=0成立,
∴方程ax2-2ax+c=0的解是x=-1.
故答案是:x=-1.
点评 本题拷出来方程的解与二次函数的关系,求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.

练习册系列答案
相关题目
5.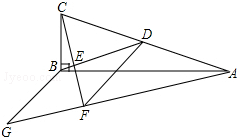 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若CF=6,AC=AF+2,则四边形BDFG的周长为( )
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若CF=6,AC=AF+2,则四边形BDFG的周长为( )
 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若CF=6,AC=AF+2,则四边形BDFG的周长为( )
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若CF=6,AC=AF+2,则四边形BDFG的周长为( )| A. | 9.5 | B. | 10 | C. | 12.5 | D. | 20 |
12.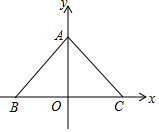 如图,坐标平面上有A(0,a)、B(-9,0)、C(10,0)点,其中a>0,若∠BAC=100°,则△ABC的外心在( )
如图,坐标平面上有A(0,a)、B(-9,0)、C(10,0)点,其中a>0,若∠BAC=100°,则△ABC的外心在( )
 如图,坐标平面上有A(0,a)、B(-9,0)、C(10,0)点,其中a>0,若∠BAC=100°,则△ABC的外心在( )
如图,坐标平面上有A(0,a)、B(-9,0)、C(10,0)点,其中a>0,若∠BAC=100°,则△ABC的外心在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.某校九年级学生从学校出发,到相距8千米的科技馆参观,第一组学生骑自行车先走,过了20分钟,第二组学生乘汽车出发,结果两组学生同学同时到达科技馆,已知第二组学生的速度是第一组学生速度的2倍,设第一组学生的速度为x千米/时,下面所列方程正确的是( )
| A. | $\frac{8}{x}$-$\frac{8}{2x}$=$\frac{1}{3}$ | B. | $\frac{8}{x}$$-\frac{8}{2x}$=20 | C. | $\frac{8}{2x}$-$\frac{8}{x}$=$\frac{1}{3}$ | D. | $\frac{8}{2x}$$-\frac{8}{x}$=20 |
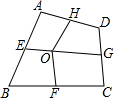 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,则S四边形DHOG为( )
如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,则S四边形DHOG为( ) 如图,在四边形ABCD中,对角线AC=4cm,BD=2cm,AC与BD垂直,M,N分别是AB、CD的中点,则MN2=5cm.
如图,在四边形ABCD中,对角线AC=4cm,BD=2cm,AC与BD垂直,M,N分别是AB、CD的中点,则MN2=5cm.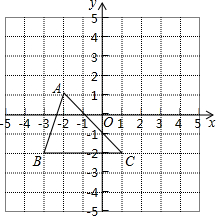 如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.