题目内容
5.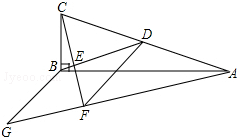 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若CF=6,AC=AF+2,则四边形BDFG的周长为( )
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若CF=6,AC=AF+2,则四边形BDFG的周长为( )| A. | 9.5 | B. | 10 | C. | 12.5 | D. | 20 |
分析 首先可判断四边形BGFD是平行四边形,再由直角三角形斜边中线等于斜边一半,可得BD=FD,则可判断四边形BGFD是菱形,设AF=x,则AC=x+2,FC=6,在Rt△ACF中利用勾股定理可求出x的值,进而得出答案.
解答 解:∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵点D是AC中点,
∴BD=DF=$\frac{1}{2}$AC,
∴四边形BGFD是菱形,
设AF=x,则AC=x+2,FC=6,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2,即x2+62=(2+x)2,
解得:x=8,
故AC=10,
故四边形BDFG的周长=4BD=2×10=20.
故选:D.
点评 本题考查了菱形的判定与性质、勾股定理及直角三角形的斜边中线的性质,解答本题的关键是判断出四边形BGFD是菱形.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
17.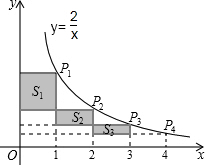 如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=( )
如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=( )
 如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=( )
如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
14.“倡导全民阅读”、“推动国民素质和社会文明程度显著提高”已成为“十三五”时期的重要工作.教育主管部门对某学校青年学校青年教师2016年度阅读情况进行了问卷调查,并将收集的数据统计如表,根据表中的信息判断,下列结论错误的是( )
| 数量/本 | 15 | 11 | 8 | 4 | 3 | 2 |
| 人数 | 8 | 6 | 5 | 10 | 4 | 7 |
| A. | 该学校中参与调查的青年教师人数为40人 | |
| B. | 该学校中青年教师2016年平均每人阅读8本书 | |
| C. | 该学校中青年教师2016年度看书数量的中位数为4本 | |
| D. | 该学校中青年教师2016年度看书数量的众数为4本 |
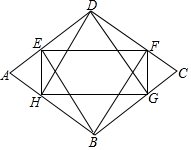 如图,在菱形ABCD中,分别过B、D作对边的垂线,垂足分别为E、F、G、H.若四边形EFGH的面积与菱形ABCD的面积之比为4:9,则sinA=$\frac{2\sqrt{2}}{3}$或$\frac{\sqrt{5}}{3}$.
如图,在菱形ABCD中,分别过B、D作对边的垂线,垂足分别为E、F、G、H.若四边形EFGH的面积与菱形ABCD的面积之比为4:9,则sinA=$\frac{2\sqrt{2}}{3}$或$\frac{\sqrt{5}}{3}$. 在平面直角坐标系中,抛物线y=ax2+bx-3经过点A(-1,0)和点B(2,-1),交y轴于点C,BD⊥x轴于点D,连接AB、AC.
在平面直角坐标系中,抛物线y=ax2+bx-3经过点A(-1,0)和点B(2,-1),交y轴于点C,BD⊥x轴于点D,连接AB、AC.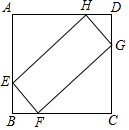 如图,正方形ABCD,AB=8,点E,F,G,H分别在正方形ABCD的边上(不与正方形的顶点重合),设BF=m,EF:FG=1:k,其中k≥1,若四边形EFGH是矩形,
如图,正方形ABCD,AB=8,点E,F,G,H分别在正方形ABCD的边上(不与正方形的顶点重合),设BF=m,EF:FG=1:k,其中k≥1,若四边形EFGH是矩形,