题目内容
11．
如图，在四边形ABCD中，对角线AC=4cm，BD=2cm，AC与BD垂直，M，N分别是AB、CD的中点，则MN2=5cm．
分析 取AD的中点H，连接MH、FH，根据三角形中位线定理求出HM、HN，根据勾股定理计算即可．
解答 解：
取AD的中点H，连接MH、FH，
则HM、HN分别是△ABD、△ADC的中位线，
则HM=$\frac{1}{2}$BD=1，HM∥BD，HN=$\frac{1}{2}$AC=2，HN∥AC，
∵AC⊥BD，
∴NM⊥HN，
∴MN2=MH2+HN2=5，
故答案为：5．
点评 本题考查的是三角形的中位线定理，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
练习册系列答案
全能测控期末小状元系列答案
相关题目
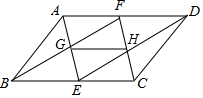如图所示，在?ABCD中，E、F分别是BC、AD的中点，AE与BF相交于点G，DE与CF相交于点H．求证：GH$\stackrel{∥}{=}$$\frac{1}{2}$AD．
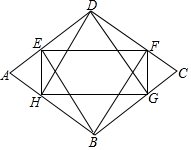如图，在菱形ABCD中，分别过B、D作对边的垂线，垂足分别为E、F、G、H．若四边形EFGH的面积与菱形ABCD的面积之比为4：9，则sinA=$\frac{2\sqrt{2}}{3}$或$\frac{\sqrt{5}}{3}$．
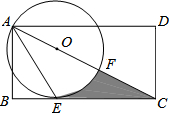如图，在矩形ABCD中，AD＞AB，AE是∠BAC的平分线交BC于点E，以AC上一点O为圆心作圆，使⊙O经过A，E两点，⊙O交AC于点F，
