题目内容
15.如图1,在△ABC中,∠ABC与∠ACB的角平分线交于O点.(1)若∠A=40°,则∠BOC=110°;
(2)若∠A=n°,则∠BOC=90+$\frac{n}{2}$°;
(3)若∠A=n°,∠ABC与∠ACB的角平分线交于O点,∠ABO的平分线与∠ACO的平分线交于点O1,…,∠ABO2016的平分线与∠ACO2016的平分线交于点O2017,则∠O2017=$\frac{1}{{2}^{2018}}$×180°+$\frac{{2}^{2018}-1}{{2}^{2018}}$n°.
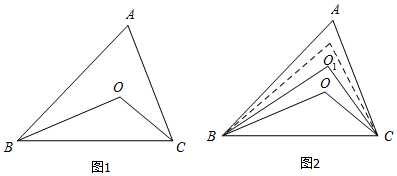
分析 (1)根据三角形内角和定理可求得∠ABC+∠ACB的度数,再根据角平分线的定义可求得∠OBC+∠OCB的度数故可得出结论;
(2)根据BO、CO分别是∠ABC与∠ACB的角平分线,用n°的代数式表示出∠OBC与∠OCB的和,再根据三角形的内角和定理求出∠BOC的度数;
(3)根据角平分线的定义和三角形的内角和即可得到结论.
解答 解:(1)∵∠A=40°,
∴∠ABC+∠ACB=140°,
∵点O是∠ABC与∠ACB的角平分线的交点,
∴∠OBC+∠OCB=70°,
∴∠BOC=110°.
故答案为:110°;
(2)∵∠A=n°,
∴∠ABC+∠ACB=180°-n°,
∵BO、CO分别是∠ABC与∠ACB的角平分线,
∴∠OBC+∠OCB=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB
=$\frac{1}{2}$(∠ABC+∠ACB)
=$\frac{1}{2}$(180°-n°)
=90°-$\frac{1}{2}$n°,
∴∠BOC=180°-(∠OBC+∠OCB)=90°+$\frac{1}{2}$n°.
故答案为:90°+$\frac{1}{2}$n°;
(3)由(2)得∠O=90°+$\frac{1}{2}$n°,
∵∠ABO的平分线与∠ACO的平分线交于点O1,
∴∠O1BC=$\frac{3}{4}$∠ABC,∠O1CB=$\frac{3}{4}$∠ACB,
∴∠O1=180°-$\frac{3}{4}$(∠ABC+∠ACB)=180°-$\frac{3}{4}$(180°-∠A)=$\frac{1}{4}$×180°+$\frac{3}{4}$n°,
同理,∠O2=$\frac{1}{8}$×180°+$\frac{7}{8}$n°,
∴∠On=$\frac{1}{{2}^{n+1}}$×180°+$\frac{{2}^{n+1}-1}{{2}^{n+1}}$n°,
∴∠O2017=$\frac{1}{{2}^{2018}}$×180°+$\frac{{2}^{2018}-1}{{2}^{2018}}$n°,
故答案为:$\frac{1}{{2}^{2018}}$×180°+$\frac{{2}^{2018}-1}{{2}^{2018}}$n°.
点评 本题考查了三角形内角和定理,角平分线定义的应用,注意:三角形的内角和等于180°.

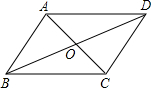 如图所示,平行四边形ABCD的对角线AC,BD交于点O,已知AD=16,BD=24,AC=12,则△OBC的周长为( )
如图所示,平行四边形ABCD的对角线AC,BD交于点O,已知AD=16,BD=24,AC=12,则△OBC的周长为( )| A. | 26 | B. | 34 | C. | 40 | D. | 52 |
| A. | $\frac{22}{7}$ | B. | tan30° | C. | 3.14 | D. | 2-1 |
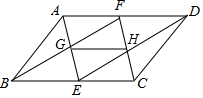 如图所示,在?ABCD中,E、F分别是BC、AD的中点,AE与BF相交于点G,DE与CF相交于点H.求证:GH$\stackrel{∥}{=}$$\frac{1}{2}$AD.
如图所示,在?ABCD中,E、F分别是BC、AD的中点,AE与BF相交于点G,DE与CF相交于点H.求证:GH$\stackrel{∥}{=}$$\frac{1}{2}$AD.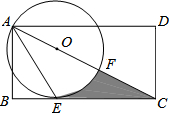 如图,在矩形ABCD中,AD>AB,AE是∠BAC的平分线交BC于点E,以AC上一点O为圆心作圆,使⊙O经过A,E两点,⊙O交AC于点F,
如图,在矩形ABCD中,AD>AB,AE是∠BAC的平分线交BC于点E,以AC上一点O为圆心作圆,使⊙O经过A,E两点,⊙O交AC于点F,