题目内容
12.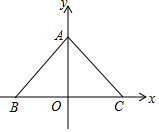 如图,坐标平面上有A(0,a)、B(-9,0)、C(10,0)点,其中a>0,若∠BAC=100°,则△ABC的外心在( )
如图,坐标平面上有A(0,a)、B(-9,0)、C(10,0)点,其中a>0,若∠BAC=100°,则△ABC的外心在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 根据钝角三角形的外心在三角形的外部即可得出结论.
解答 解:∵B(-9,0)、C(10,0),
∴△ABC的外心在直线x=$\frac{1}{2}$上.
∵∠BAC=100°,
∴△ABC的外心在三角形的外部,
∴△ABC的外心在第四象限.
故选D.
点评 本题考查的是三角形的外接圆与外心,熟知钝角三角形的外心在三角形的外部是解答此题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
17.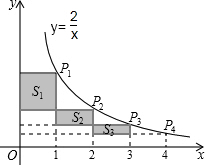 如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=( )
如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=( )
 如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=( )
如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
4.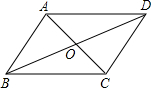 如图所示,平行四边形ABCD的对角线AC,BD交于点O,已知AD=16,BD=24,AC=12,则△OBC的周长为( )
如图所示,平行四边形ABCD的对角线AC,BD交于点O,已知AD=16,BD=24,AC=12,则△OBC的周长为( )
 如图所示,平行四边形ABCD的对角线AC,BD交于点O,已知AD=16,BD=24,AC=12,则△OBC的周长为( )
如图所示,平行四边形ABCD的对角线AC,BD交于点O,已知AD=16,BD=24,AC=12,则△OBC的周长为( )| A. | 26 | B. | 34 | C. | 40 | D. | 52 |
2.函数y=$\sqrt{x-2}$中自变量x的取值范围是( )
| A. | x>2 | B. | x≥2 | C. | x≤2 | D. | x≠2 |
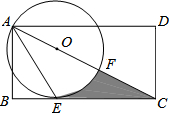 如图,在矩形ABCD中,AD>AB,AE是∠BAC的平分线交BC于点E,以AC上一点O为圆心作圆,使⊙O经过A,E两点,⊙O交AC于点F,
如图,在矩形ABCD中,AD>AB,AE是∠BAC的平分线交BC于点E,以AC上一点O为圆心作圆,使⊙O经过A,E两点,⊙O交AC于点F,


