题目内容
11.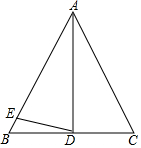 如图,在△ABC中,∠B=∠C,AD平分∠BAC,∠CAD=26°,∠AED=∠ADE,求∠BDE的度数.
如图,在△ABC中,∠B=∠C,AD平分∠BAC,∠CAD=26°,∠AED=∠ADE,求∠BDE的度数.
分析 首先两次运用三角形外角的性质得∠EDC=(∠B+∠CAD-∠EDB)-∠B=26°-∠EDB,然后移项可得结果.
解答 解:∵∠EDB=∠AED-∠B,∠ADE=∠AED,
∴∠EDB=∠ADE-∠C,
∵∠ADE=∠C+∠CAD-∠EDB,
∴∠EDB=(∠C+∠CAD-∠EDB)-∠C=26°-∠EDB,
即2∠EDB=26°
∴∠EDB=13°.
故∠EDB的度数为13°.
点评 本题考查了等腰三角形的性质及三角形内角和定理,三角形外角的性质;解决本题的关键是利用外角和相等的角得到所求角和已知角之间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.在一次“数学与生活”知识竞赛中,竞赛题共26道,每道题都给出4个答案,其中只有一个答案正确,选对得4分,不选或选错扣2分,得分不低于70分得奖,那么得奖至少应选对( )道题.
| A. | 22 | B. | 21 | C. | 20 | D. | 19 |
3.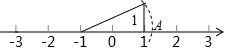 如图,在数轴上点A表示的数为a,则a的值为( )
如图,在数轴上点A表示的数为a,则a的值为( )
 如图,在数轴上点A表示的数为a,则a的值为( )
如图,在数轴上点A表示的数为a,则a的值为( )| A. | $\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | 1-$\sqrt{5}$ | D. | -1+$\sqrt{5}$ |
 如图,点B在AD的延长线上,DE∥AC,若∠C=50°,∠BDE=60°,则∠CDB=110°.
如图,点B在AD的延长线上,DE∥AC,若∠C=50°,∠BDE=60°,则∠CDB=110°.
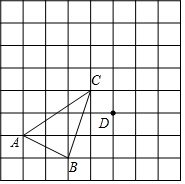 在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移后得△DEF,使点A的对应点为点D,点B的对应点为点E.
在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移后得△DEF,使点A的对应点为点D,点B的对应点为点E.