题目内容
1.(1)计算:|-4|-(-2)2+$\sqrt{9}$-($\frac{1}{2}$)0(2)解不等式组$\left\{\begin{array}{l}{3x-x≥2}\\{\frac{1+2x}{3}>x-1}\end{array}$.
分析 (1)原式第一项利用绝对值的代数意义化简,第二项利用乘方的意义计算,第三项化为最简二次根式,最后一项利用零指数幂法则计算,即可得到结果.
(2)先求出两个不等式的解集,再求其公共解.
解答 解:(1)原式=4-4+3-1=2;
(2)$\left\{\begin{array}{l}{3x-x≥2①}\\{\frac{1+2x}{3}>x-1②}\end{array}\right.$
解不等式①得,x≥1,
解不等式②得,x<4,
所以不等式组的解集是1≤x<4.
点评 本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).也考查了实数的运算.

练习册系列答案
相关题目
9.关于x的不等式组$\left\{\begin{array}{l}{x-a≥0}\\{3-2x>-1}\end{array}\right.$的整数解共有5个,则a的取值范围( )
| A. | a=-3 | B. | -4<a<-3 | C. | -4≤a<-3 | D. | -4<a≤-3 |
16. 如图,圆锥的底面半径为2,母线长为6,则侧面积为( )
如图,圆锥的底面半径为2,母线长为6,则侧面积为( )
 如图,圆锥的底面半径为2,母线长为6,则侧面积为( )
如图,圆锥的底面半径为2,母线长为6,则侧面积为( )| A. | 4π | B. | 6π | C. | 12π | D. | 16π |
1.已知二次函数y1=ax2+bx+c(b≠c)图象的最高点坐标为(-2,4),则一次函数y2=(b-c)x+b2-4ac图象可能在( )
| A. | 一、二、三象限 | B. | 一、二、四象限 | C. | 一、三、四象限 | D. | 二、三、四象限 |
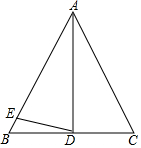 如图,在△ABC中,∠B=∠C,AD平分∠BAC,∠CAD=26°,∠AED=∠ADE,求∠BDE的度数.
如图,在△ABC中,∠B=∠C,AD平分∠BAC,∠CAD=26°,∠AED=∠ADE,求∠BDE的度数.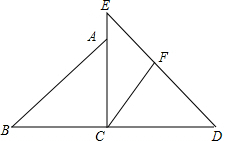 将一副三角尺拼成如图所示,∠BAC=45°,∠D=30°,∠BCA=∠DCE=90°,过点C作CF∥AB,交DE于点F,则∠EFC=75度.
将一副三角尺拼成如图所示,∠BAC=45°,∠D=30°,∠BCA=∠DCE=90°,过点C作CF∥AB,交DE于点F,则∠EFC=75度.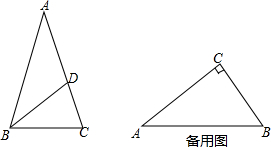 我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.
我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.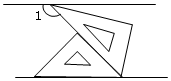 如图,将一副三角板和一张对边平行的纸条按下列方式摆放:含30°角的直角三角板的斜边与含45°角的直角三角板一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是135°.
如图,将一副三角板和一张对边平行的纸条按下列方式摆放:含30°角的直角三角板的斜边与含45°角的直角三角板一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是135°.