题目内容
6.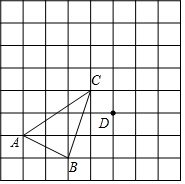 在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移后得△DEF,使点A的对应点为点D,点B的对应点为点E.
在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移后得△DEF,使点A的对应点为点D,点B的对应点为点E.(1)画出△DEF;
(2)连接AD、BE,则线段AD与BE的关系是平行且相等;
(3)求△DEF的面积.
分析 (1)将点B、C均向右平移4格、向上平移1格,再顺次连接可得;
(2)根据平移的性质可得;
(3)割补法求解即可.
解答  解:(1)如图所示,△DEF即为所求;
解:(1)如图所示,△DEF即为所求;
(2)由图可知,线段AD与BE的关系是:平行且相等,
故答案为:平行且相等;
(3)S△DEF=3×3-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×3=$\frac{7}{2}$.
点评 本题考查了利用平移变换作图,平移的性质,熟练掌握网格结构,准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
16.已知点A(-1,-5)和点B(2,m),且AB平行于x轴,则B点坐标为( )
| A. | (2,-5) | B. | (2,5) | C. | (2,1) | D. | (2,-1) |
16. 如图,圆锥的底面半径为2,母线长为6,则侧面积为( )
如图,圆锥的底面半径为2,母线长为6,则侧面积为( )
 如图,圆锥的底面半径为2,母线长为6,则侧面积为( )
如图,圆锥的底面半径为2,母线长为6,则侧面积为( )| A. | 4π | B. | 6π | C. | 12π | D. | 16π |
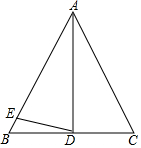 如图,在△ABC中,∠B=∠C,AD平分∠BAC,∠CAD=26°,∠AED=∠ADE,求∠BDE的度数.
如图,在△ABC中,∠B=∠C,AD平分∠BAC,∠CAD=26°,∠AED=∠ADE,求∠BDE的度数.