��Ŀ����
 ��ѧ��С����ѧ�������εĽ�ƽ���ߺ�����������4�����⣬����һ����룬��ͬ������
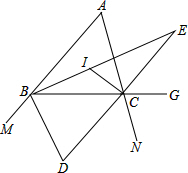
��ѧ��С����ѧ�������εĽ�ƽ���ߺ�����������4�����⣬����һ����룬��ͬ��������ͼ����ABC����I�ǡ�ABC���ACBƽ���ߵĽ��㣬��D�ǡ�MBC���NCBƽ���ߵĽ��㣬��E�ǡ�ABC���ACGƽ���ߵĽ��㣮
���⣨1��������BAC=50�㣬���BIC=
���⣨2�����������BEC���BAC��������ϵ����˵�����ɣ�
���⣨3��������BAC=x�㣨0��x��90������ACB����
���⣨4��������BDE�д���һ���ڽǵ�����һ���ڽǵ������������BAC�Ķ�����
���㣺�������ڽǺͶ���,�����ε��������
ר�⣺
��������1����֪��I������B��Cƽ���ߵĽ��㣬�ʡ�BIC=180��-����IBC+��ICB��=180��-
����ABC+��ACB��=180��-
��180��-��A��=90+
��BAC���ɴ˿����BIC����ΪBE��BD�ֱ�Ϊ��ABC���ڽǡ����ƽ���ߣ��ʡ�DBI=90�㣬ͬ����DCI=90�㣬���ı���CDBI�У���֤��BDC=180��-��BIC=90-
��BAC���ɴ˿����BDC��
��2���ڡ�BDE�У���DBI=90�㣬�ʡ�BEC=90��-��BDC=
��BAC��
��3����CE��ABʱ����BEC=
��ABC���ɣ�3����֪����ABC=��BAC����ACB=
��180-��BAC����
��4��������֪����BDE��ֱ�������Ρ�D+��E=90������EBD=3��Dʱ��BAC=120�㣻����EBD=3��Eʱ��BAC=60�㣻����D=3��Eʱ��BAC=45�㣻����E=3��Dʱ��BAC=135�㣮
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��2���ڡ�BDE�У���DBI=90�㣬�ʡ�BEC=90��-��BDC=
| 1 |
| 2 |
��3����CE��ABʱ����BEC=
| 1 |
| 2 |
| 1 |
| 2 |
��4��������֪����BDE��ֱ�������Ρ�D+��E=90������EBD=3��Dʱ��BAC=120�㣻����EBD=3��Eʱ��BAC=60�㣻����D=3��Eʱ��BAC=45�㣻����E=3��Dʱ��BAC=135�㣮
����⣺��1���ߵ�I������B��Cƽ���ߵĽ��㣬
���BIC=180��-����IBC+��ICB��
=180��-
����ABC+��ACB��
=180��-
��180��-��A��
=90+
��BAC=115�㣻
��BE��BD�ֱ�Ϊ��ABC���ڽǡ����ƽ���ߣ�
���DBI=90�㣬ͬ����DCI=90�㣬
���ı���CDBI�У���BDC=180��-��BIC=90��-
��BAC=65�㣻
��2����BEC=
��BAC��
֤�����ڡ�BDE�У���DBI=90�㣬
���BEC=90��-��BDC
=90��-��90��-
��BAC��
=
��BAC��
��3������ACB���ڣ�180-2x����ʱ��CE��AB���������£�
��CE��AB��
���ACE=��A=x�㣬
��CE�ǡ�ACG��ƽ���ߣ�
���ACG=2��ACE=2x�㣬
���ABC=��ACG-��BAC=2x��-x��=x�㣬
���ACB=180��-��BAC-��ABC=��180-2x���㣮
��4��������֪����BDE��ֱ�������Ρ�D+��E=90��
����EBD=3��Dʱ��BAC=120�㣻
����EBD=3��Eʱ��BAC=60�㣻
����D=3��Eʱ��BAC=45�㣻
����E=3��Dʱ��BAC=135�㣮
�ʴ�Ϊ����1��115��65����2����BEC=
��BAC����3��180-2x����4������EBD=3��Dʱ��BAC=120�㣻����EBD=3��Eʱ��BAC=60�㣻����D=3��Eʱ��BAC=45�㣻����E=3��Dʱ��BAC=135�㣮
���BIC=180��-����IBC+��ICB��
=180��-
| 1 |
| 2 |
=180��-
| 1 |
| 2 |
=90+
| 1 |
| 2 |
��BE��BD�ֱ�Ϊ��ABC���ڽǡ����ƽ���ߣ�
���DBI=90�㣬ͬ����DCI=90�㣬
���ı���CDBI�У���BDC=180��-��BIC=90��-
| 1 |
| 2 |
��2����BEC=
| 1 |
| 2 |
֤�����ڡ�BDE�У���DBI=90�㣬
���BEC=90��-��BDC
=90��-��90��-
| 1 |
| 2 |
=
| 1 |
| 2 |
��3������ACB���ڣ�180-2x����ʱ��CE��AB���������£�
��CE��AB��
���ACE=��A=x�㣬
��CE�ǡ�ACG��ƽ���ߣ�
���ACG=2��ACE=2x�㣬
���ABC=��ACG-��BAC=2x��-x��=x�㣬
���ACB=180��-��BAC-��ABC=��180-2x���㣮
��4��������֪����BDE��ֱ�������Ρ�D+��E=90��
����EBD=3��Dʱ��BAC=120�㣻
����EBD=3��Eʱ��BAC=60�㣻
����D=3��Eʱ��BAC=45�㣻
����E=3��Dʱ��BAC=135�㣮
�ʴ�Ϊ����1��115��65����2����BEC=
| 1 |
| 2 |
���������⿼���������ε��ڽǡ����ƽ���ߵļнǴ�С��ԭ�������ڽǵĹ�ϵ��Ҫ��������������ڽǺͶ�������ƽ��������ת����

��ϰ��ϵ�д�
�����Ŀ



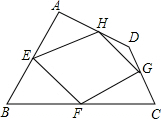 ��֪����ͼ���ı���ABCD�������ϵ��е�ֱ�ΪE��F��G��H��˳������EF��FG��GH��HE���õ��ı���EFGH�����ı���ABCD���е��ı��Σ���
��֪����ͼ���ı���ABCD�������ϵ��е�ֱ�ΪE��F��G��H��˳������EF��FG��GH��HE���õ��ı���EFGH�����ı���ABCD���е��ı��Σ���