题目内容
已知x2+3x-2=0,y2+3y-2=0,且x≠y,求
+
的值.
| y |
| x |
| x |
| y |
考点:根与系数的关系
专题:计算题
分析:根据条件,可把x、y可看作方程t2+3t-2=0的两根,根据根与系数的关系得x+y=-3,xy=-2,再把
+
变形得到
,然后利用整体代入的方法计算.
| y |
| x |
| x |
| y |
| (x+y)2-2xy |
| xy |
解答:解:∵x2+3x-2=0,y2+3y-2=0,
∴x、y可看作方程t2+3t-2=0的两根,
∴x+y=-3,xy=-2,
∴
+
=
=
=
=-
.
∴x、y可看作方程t2+3t-2=0的两根,
∴x+y=-3,xy=-2,
∴
| y |
| x |
| x |
| y |
| x2+y2 |
| xy |
| (x+y)2-2xy |
| xy |
| (-3)2-2×(-2) |
| -2 |
| 13 |
| 2 |
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
 如图,在△ABC中,D、E分别是AB、AC的中点,连结DE,若BC=2,则DE=
如图,在△ABC中,D、E分别是AB、AC的中点,连结DE,若BC=2,则DE= ”表示(表示输入、输出操作);“处理框”用“
”表示(表示输入、输出操作);“处理框”用“ ”表示(表示数据处理和运算);“判断框”用“
”表示(表示数据处理和运算);“判断框”用“ ”表示(根据条件决定执行两条路径中的某一条)
”表示(根据条件决定执行两条路径中的某一条)
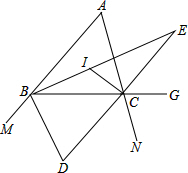 好学的小红在学完三角形的角平分线后,钻研了下列4个问题,请你一起参与,共同进步.
好学的小红在学完三角形的角平分线后,钻研了下列4个问题,请你一起参与,共同进步.
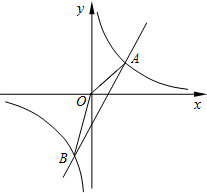 如图,已知反比例函数y1=
如图,已知反比例函数y1=